|
|
|
|||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||
|
|
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
| |||||||||||||||||||||||||||||||||
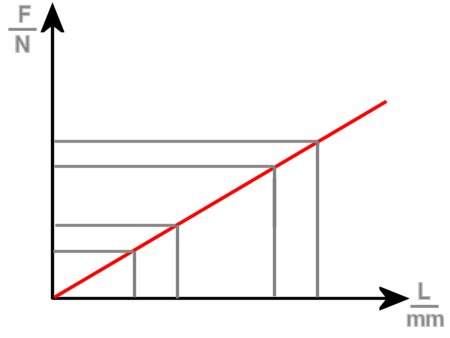
| ΔF remains constant. |
In this case, the force increases evenly with the distance that the spring is compressed or stretched. We speak here, of a characteristic curve. If the angle of the linear slope to the X-axis is greater, then this is a relatively harder spring (high spring-rate) than if the angle is smaller.
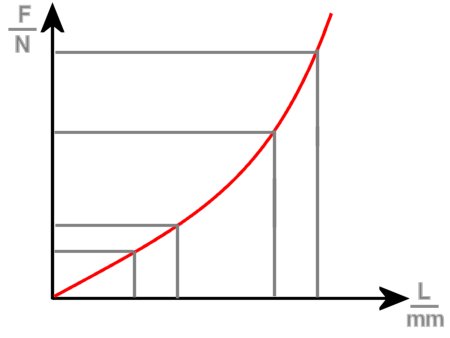
| ΔF increases. |
In this case, the spring-rate is low, with small changes in the length, it then becomes higher and higher. This is typical for a progressive characteristic curve.
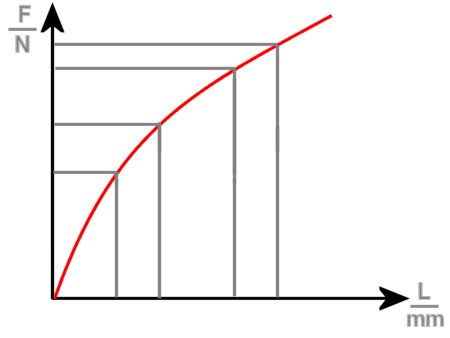
| ΔF decreases. |
In this case, the additional spring force necessary decreases with the increasing length of the curve, this is described as being a degressive characteristic curve. This interpretation is seldom found in the motor vehicle field. In the field of chassis and suspension, the springing e.g., is often progressive.
The identifiers for the spring-rate are usually: c, k, and very occasionally, D. The formula and the conversion used is:
| c | = | ΔF / ΔL | (N/mm) |
| ΔF | = | c * ΔL | (N) |
| ΔL | = | ΔF / c | (mm) |
A spring, when strained, can take on energy. How it is strained, depends on what type of spring it is. We'll be concentrating on the pressure spring, which is more often found in the motor vehicle. When it is compressed, mechanical force is applied, i.e., energy is put in. To understand this, take a look at a pendulum-clock with weights. The lifting of the weights corresponds to the applied force, which in this case, we'll call potential energy.
To be able to calculate more easily, we'll assume a linear characteristic curve and because the force still doesn't remain constant, we'll reckon with the average value:
The difference between the force-begin and the force-end is defined as ?F. Half this difference expresses the average force, which we'll assume has been applied over the entire change of length.
Instead of the force difference, we can now insert the product from the spring-rate and the spring-travel.
Square this off, and the new formula, together with it's conversions is finished:
| Epot | = | c * ΔL2 / 2 | (Nm) |
| c | = | Epot * 2 / ΔL2 | (N/m) |
| ΔL | = | (Epot * 2 / c)-2 | (m) |
| 1 Nm = 1 J(oule) |
| Next page |
2001-2015 Copyright programs, texts, animations, pictures: H. Huppertz - E-Mail
Translator: Don Leslie - Email: lesdon@t-online.de