|
| 
|
Reciprocating piston engine
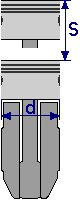
The single cylinder capacity is calculated as the volume of the cylinder. However, here the cylinder height s is assumed to be the distance between the top and bottom dead center. It is therefore an imaginary cylinder
between the two piston positions. The displacement therefore depends exclusively on the cylinder diameter and the
crank angle of the crankshaft.
The largest total displacement of a petrol engine is probably 27 liters and dates back to 1923. As diesel engines are also used in large ships, their single displacement can sometimes reach
one cubic meter (1000 liters) or more.
Vh =
A · s | Vh
A = 
s | Vh
s = 
A |
d²·
Vh
= ·s
·s
4 | 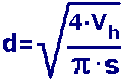
|
4·Vh
s=
d²· |
VH = Vh·z | V
H
Vh = 
z
|
VH
z = 
Vh
|
| d | Piston diameter | mm, cm, dm |
| A | Piston surface | mm2, cm2, dm2 |
| h | Displacement | mm, cm, dm |
| Vh | Single displacement | mm3, cm3, dm3 |
| z | Number of cylinders | |
| VH | Total displacement | mm3, cm3, dm3 |
  
| Short-stroke engine, square-shaped,
long-stroke engine |
The stroke is compared with the bore. This bore-stroke ratio influences the operating behavior of the engine. While the short-stroke piston (left image) has less stroke than bore, the opposite is true for the long-stroke
piston (right image). If both are approximately equal, this is referred to as a square cross-section.
| Particularly short-stroke engines in Formula 1 |
While long-stroke engines tend to excel in terms of torque in the lower speed range, short-stroke engines are capable of particularly high speeds and large valve openings. An extreme example was Formula 1 (2007) with
a 2.4-liter V8 and approximately 98 mm bore and 40 mm stroke. The latter ensures that the average piston speed
does not rise significantly above 25 m/s despite a maximum speed of 19,000 rpm. To keep the weight of the pistons low, there is no oil scraper ring, almost no piston skirt, and a piston pin that is greatly shortened and
attached directly below the piston bottom.
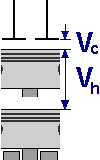
The compression ratio is the ratio of the total cylinder chamber before compression (displacement + compression chamber) to the remaining chamber after compression (compression chamber).
| Higher compression ratio | | Higher final compression pressure |
| Higher octane number requirement |
Vh + Vc
ε = 
Vc |
Vh
Vc = 
ε - 1 |
Vh = Vc · (ε - 1) |
| Vh | Displacement of one cylinder | mm3, cm3, dm3 |
| Vh | Compression chamber of a cylinder | mm3, cm3, dm3 |
| ε | Compression ratio | |
The compression ratio can be determined by level calibration. To do this, the piston of the cylinder to be measured must be set to ignition top dead center and filled with liquid via the spark plug hole. This can be done with
a spraying device and accurate recording of the filling quantity up to and including the candle hole. The motor must be positioned so that it is vertical and no air bubbles form inside.
The same exercise follows with the piston at UT. The problem is actually closing both valves. Perhaps this can be achieved by removing the overhead camshaft or rocker arm(s). However, one could also calculate using
the single-stroke displacement specified by the manufacturer.
Now all that remains is to subtract the volume of the candle hole. Perhaps you could immerse an original spark plug up to the sealing ring in water and measure the increase in liquid volume. The final calculation is
performed by dividing the two values by each other (see above).
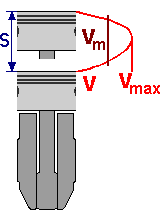
The average piston speed is the distance the piston would travel in a given unit of time if it maintained the same speed throughout the entire stroke. In reality, however, the piston speed (light red) changes from zero at the
dead centers to the maximum piston speed slightly above the center. This is approximately 1.6 times the average piston speed (dark red).
s · n
vm = 
30.000 |
vm · 30.000
s = 
n |
vm · 30.000
n = 
s |
| s | Stroke of one cylinder | mm, cm, dm |
| n | Engine speed | 1/min |
| vm | Average piston speed | m/s |
|
|