Polynom könnte vom Griechischen her 'Viele Namen' heißen, würde aber neudeutsch mit 'Mehrgliedriger Term' zu übersetzen sein. Dabei ist natürlich die rechte Seite der Gleichung gemeint, die ja nur aus Summanden besteht. Bei diesen kommt es weniger auf die Konstanten an, sondern die Stellung eines jeden Summanden richtet sich nach dem Exponenten beim jeweiligen 'x'.

Oben ist die zweite Zeile nur ein Beispiel für ein Polynom. Die oberste Zeile erklärt es umfassend. Die beginnt mit der Konstanten ohne die Variable 'x' und steigert sowohl deren Exponent als auch den Index an der jeweiligen Konstanten bis zur Anzahl n. Hier wird dann auch deutlich, warum man von einer 'Abbrechenden Potenzreihe' sprechen kann.

Es gibt also eine bestimmte Ordnung in einem Polynom, nämlich, dass die Exponenten an den Summanden der Reihe nach steigend angeordnet sein müssen. Manche haben spezielle Bezeichnungen. So hat das oben bis zum zweiten reichende den Zusatz 'quadratisch'. Käme auch noch eine '3' als Exponent vor, hieße es 'kubisch'.

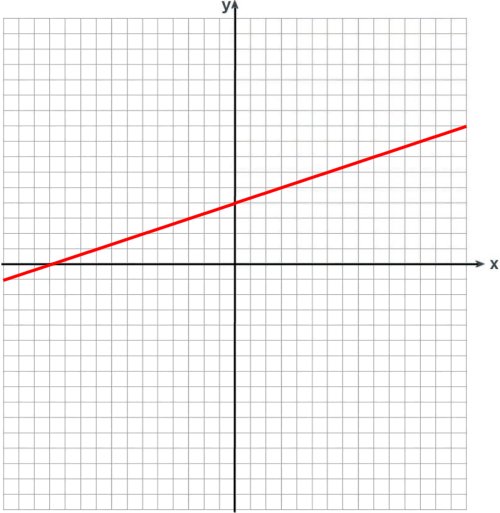
Eigentlich ist also das Polynom nur der Teil hinter dem Gleichheitszeichen. Steht ein 'f(x) =' oder 'y =' davor, wird daraus eine Funktion, die sich auch graphisch darstellen lässt. Das Bild oben entspricht

f(x) = 1/3 x +4

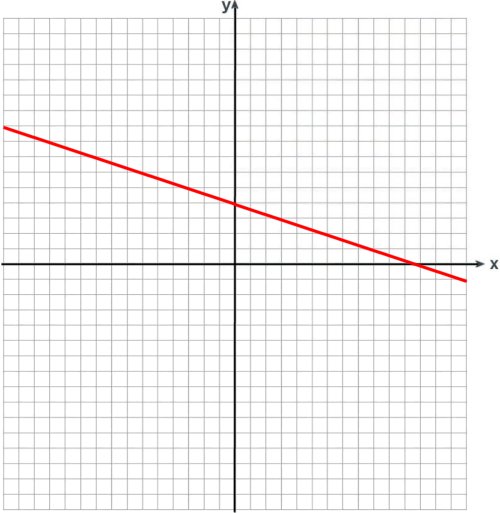
wobei die Konstante '+4' den Schnittpunkt mit der y-Achse angibt und der Koeffizient '1/3' die Steigung, also '3' in x- und '1' in y-Richtung. Ist die Steigung negativ, so ergibt sich der Verlauf unten. Man bezeichnet solche Funktionen auch als 'linear'.

Es gibt noch einfachere Polynomfunktionen, z.B.

f(x) = 2

Da hier kein x-Wert angegeben ist, nimmt man dessen Koeffizienten mit '0' an. Damit wird auch die Steigung null, also ist der Graph dieser Funktion eine Parallele zur x-Achse mit Schnittpunkt durch y = 2.

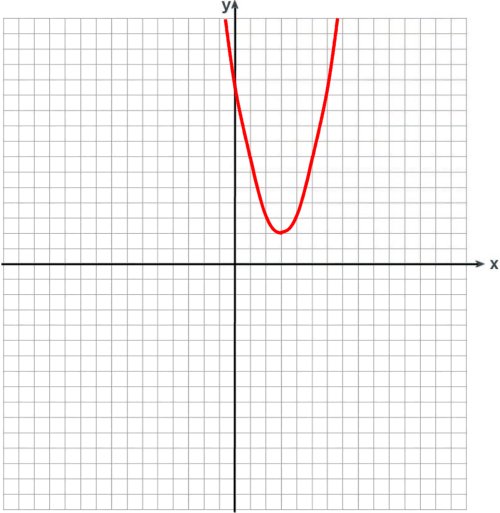
f(x) = x² - 6x + 11

Das ist jetzt ein Beispiel für eine quadratische Polynom-Funktion. Es geht nur bis zum Quadrat von x und bricht dann ab. Darüber sehen Sie den Graphen der Funktion, der sich hierbei immer als Parabel ergibt. Bei positivem x² einschließlich dem Koeffizienten ist die Parabel wie hier nach oben, bei negativem nach unten geöffnet.

Eine Möglichkeit, aus der Funktionsvorschrift die Lage z.B. des Scheitelpunktes zu finden, ist, die erste Ableitung zu bilden:

f'(x) = 2x - 6

Die erste Ableitung wird in den Kapiteln Funktionen 4 und 5 erklärt.

Wenn Sie jetzt für 'x' eine '3' einsetzen, wird f'(x) null. D.h. der Scheitelpunkt liegt bei x = 3. Setzt man die 3 in obige Funktion ein, erhält man:

f'(x) = 9 - 18 + 11

was '2' ergibt. Das entspricht also dem y-Wert für den Scheitelpunkt. Durch Einsetzen von '4'' für 'x' erhält man '3', die '5' ergibt '6' und die '6' offenbart sogar mit der '11' den Durchgang durch die y-Achse, denn alle Werte können natürlich entlang der Mittellinie der Parabel gespiegelt werden.

Hier zeigt sich schon ein Phänomen der Polynomfunktionen, nämlich dass sie maximal so viele Nullstellen haben können, wie Summanden vorhanden sind, wobei die Konstante nicht mitzählt. Wäre also unsere Parabel weiter unten angeordnet, könnte sie eine oder sogar zwei Nullstellen haben, aber mehr auch nicht.