|
|
Kfz-Technik - Leistung
Drehmoment
| Mögliche Anzugsdrehmomente in Nm |
| Bolzen | 6.9 | 8.8 | 10.9 | 12.9 |
| M 8 | 19,6 | 24,5 | 34,3 | 39,2 |
| M 10 | 39,2 | 44,1 | 63,8 | 78,5 |
| M 12 | 68,7 | 78,5 | 113,0 | 137,0 |
| M 14 | 108,0 | 128,0 | 181,0 | 216,0 |
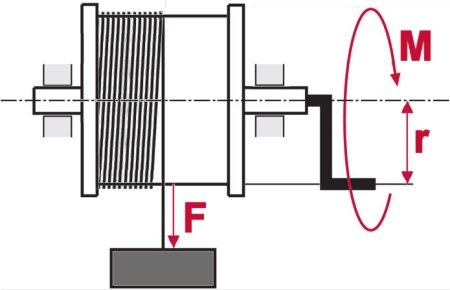
Kraft, die an einem Hebelarm ansetzt, bewirkt eine Drehbewegung. Je länger der Hebelarm und/oder je größer die Kraft, um so größer ist die Drehkraft
(das Drehmoment).
1 foot·pound (ft·lbs) = 1,35 Nm
1 Nm = 0,74 ft·lbs |
M = F · r | M
F = 
r | M
r = 
F |
| F | Kraft | N |
| r | Hebelarm | m |
| M | Drehmoment | Nm |
| n | Drehzahl | 1/min |
| P | Leistung | kW |
Pe·9550
M = 
n | M·n
Pe = 
9550 |
Pe·9550
n = 
M |
| Wie erklärt sich die Zahl 9550? |
| P = F · v | Wir gehen von dieser Formel aus. |
| F · d ·  · n · n |
| P = |
|
| 60 |
| Die Geschwindigkeit v wird ersetzt durch die Drehzahl n mal dem Kreisumfang d ·  . Die Drehzahl wird pro Minute, die
Geschwindigkeit pro Sekunde gemessen. Dadurch ergibt sich die Teilung durch 60. . Die Drehzahl wird pro Minute, die
Geschwindigkeit pro Sekunde gemessen. Dadurch ergibt sich die Teilung durch 60. |
| M · 2 ·  · n · n |
| P = |
|
| 60 |
| Der Durchmesser d wird durch den doppelten Radius 2 · r ersetzt. Dann ergibt sich das Drehmoment M aus der Kraft mal dem Radius F ·
r. |
| Soll die Leistung in kW ausgegeben werden, kommt unter dem Bruchstrich der Faktor 1000 hinzu. 1000 · 60 / 2 ·  ergibt dann den
Umrechnungsfaktor 9550, wenn man ergibt dann den
Umrechnungsfaktor 9550, wenn man  als 3,14 nimmt und entsprechend abrundet. als 3,14 nimmt und entsprechend abrundet.
|
M2 = M1 · i | M
2
M1 = 
i | M
2
i = 
M1 |
| M1 | Drehmoment (Eingang) | Nm |
| M2 | Drehmoment (Ausgang) | Nm |
| i | Übersetzung | |
Druck
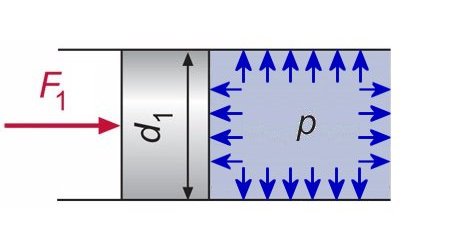
Der Druck entspricht der Kraft, die senkrecht auf die Flächeneinheit wirkt. Hier wird die Kraft auf die gedrückte Fläche bezogen, also durch die Fläche
geteilt. Beim Absolutdruck geht man von 0 bar aus. Dies ist
gleichzeitig auch der maximal (theoretisch) erreichbare Unterdruck. Auf Meereshöhe herrscht Atmosphärendruck von genau 1013 hPa. Alle Messgeräte
und -werte in der Technik geben den Relativdruck an. Dieser
geht aus vom Atmosphärendruck.
F
p = 
A |
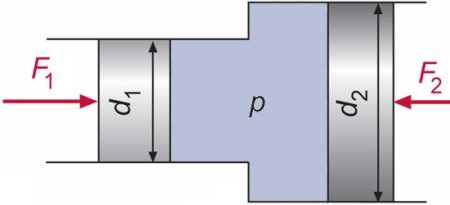
F = p · A | F
A = 
p |
| d | Durchmesser | mm, cm, dm, m |
| A | Durchmesser | mm2, cm2, dm2, m2 |
| p | Druck | bar, N/cm2, Pa, hPa |
| Umrechnungen |
| 1 bar = 10 N/cm² |
| 1 Pascal = 1 N/m2 |
| 1 bar = 100.000 Pascal (Pa) |
| 1 bar = 1.000 Hektopascal (hPa) |
| 1 mbar = 1 Hektopascal (hPa) |
|
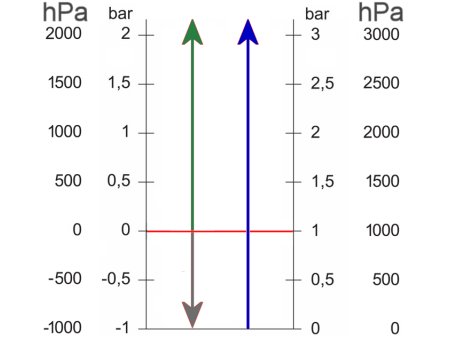
Relativdruck |
Absolutdruck |
Unterdruck,
negativer Überdruck |
| Luftdruck und Temperatur sinken in
größerer Höhe. |
Einspritzmenge
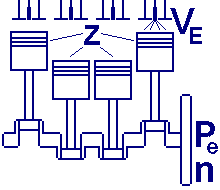
Wenn man die Reichweite eines modernen Fahrzeugs ansieht und diese auf die Umdrehungen des Motors oder sogar auf jeden einzelnen Zylinder
bezieht, dann wird da ein unvorstellbar kleines Volumen vor jedem
Arbeitstakt eingespritzt. Die Leistung moderner Technik wird vollends deutlich, wenn sich die Mengen bei verschiedenen Gaspedalstellungen nur um
Bruchteile eines Kubikmillimeters unterscheiden.
Viertaktmotor |
| Pe · be · 1000
|
| VE = |  |
|  · n · z · 30* · n · z · 30*
|
|
| Pe · be · 1000
|
| n = |  |
| VE ·  · z ·
30* · z ·
30* |
|
| VE ·  · n · z
· 30* · n · z
· 30* |
| Pe = |  |
| be · 1000 |
|
| VE ·  · n · z
· 30* · n · z
· 30* |
| be = |  |
| Pe · 1000 |
|
| * beim Zweitaktmotor hier 60 einsetzen! |
| Pe | Effektive Leistung | kW |
| n | Motordrehzahl | 1/min |
| z | Zylinderzahl | |
| be | Spezifischer Kraftstoffverbrauch | kW |
| ρ | Dichte des Kraftstoffs | g/kWh |
| Ve | Einspritzmenge | mm3 |
Mittlere Gasgeschwindigkeit
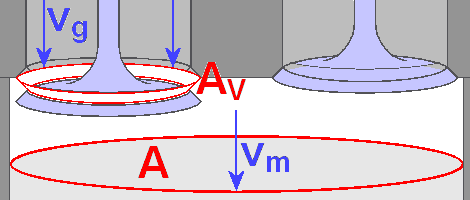
Wenn man einmal den Querschnitt der Ventilöffnung ermittelt hat, kann man ihn zum Zylinderquerschnitt ins Verhältnis setzen. Unter der Annahme, dass
genau die durch den Kolben verdrängten Gase den Zylinder
verlassen bzw. angesaugt werden, ist das Verhältnis der Querschnitte exakt umgekehrt dem der mittleren Geschwindigkeiten.
| vg | | A |
 | = |  |
| vm | | Av |
|
| vm · A |
| vg = |  |
| Av |
| | vm · A |
| Av = |  |
| vg |
|
| | vg · Av |
| vm = |  |
| A |
|
| Ae | Zylinder-Querschnittsfläche | mm3, cm3, dm3 |
| VV | Ventil-Öffnungsfläche | mm3, cm3, dm3 |
| vm | Mittlere Kolbengeschwindigkeit | m/s |
| vG | Gasgeschwindigkeit | m/s |
Leistung (mechanisch)
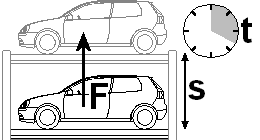
Leistung ist physikalische Arbeit, die in einer bestimmten Zeit geleistet wird. In den unten stehenden Formeln wird sie in Nm/s angegeben. Das ist exakt
die Einheit für
ein Watt. 736 davon ergeben 1 PS, was für die Pferdestärke steht, die alte Einheit. Die neue ist nach James Watt benannt, der die Dampfmaschine
industriekompatibel gemacht hat. Der hat auch die Einheit PS erfunden.
Interessant ist, dass heutige Pferde kurzfristig sogar deutlich über 2 PS leisten können. Wahrscheinlich aber hat James Watt 1765 die
Dauerleistung der Pferde im Bergwerk über bis zu 10 Stunden gemeint.
F·s
P = 
t |
F·s
t = 
P |
P·t
F = 
s |
P·t
s = 
F
|
| F | Kraft | n |
| s | Weg | m |
| t | Zeit | s |
| W | Arbeit | J, Nm |
| P | Leistung | W, Nm/s |
| v | Geschwindigkeit | m/s |
W
P = 
t |
W = P · t | W
t = 
P |
| P = F · v | P
F = 
v |
P
v = 
F |
Leistung (effektiv)
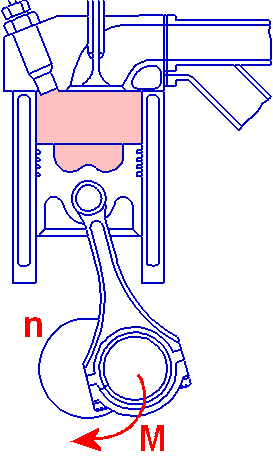
Die effektive Motorleistung wird bei Prüfstandsversuchen an der Kupplung ermittelt oder durch Abzug der Verluste im Antriebsstrang aus der Radleistung
berechnet. Leistungsangaben von Oldtimern sind mit Vorsicht
zu genießen. Bei der US-Angabe 'SAE-PS' ist die Leistung theoretisch ohne Lüfter, Kühlmittelumlauf, Luftfilter, Generator und Rückstau in der
Abgasanlage ermittelt worden. Italienische 'CUNA-PS' sind nicht ganz so
optimistisch, wurden doch hier nur Luftfilter und Abgasanlage entfernt. In beiden Fällen ist jedoch eine höhere Leistungsangabe als bei 'DIN-PS' zu
erwarten.
| Die Drehzahl, bei der die höchste Leistung erreicht wird, ist die Nenndrehzahl. |
M·n
Pe = 
9550 | Pe·9550
M = 
n
| Pe·9550
n = 
M |
| M | Drehmoment (Kurbelwelle) | Nm |
| n | Drehzahl (Kupplung) | 1/min |
| P | Leistung (effektiv) | W, Nm/s |
| Die Pferdestärke (1 'PS' = 0,736 kW) als Leistungseinheit ist megaout. Es kennzeichnet eher
die Dauerleistung eines Pferdes. Kurzzeitig schaffen geeignete
Exemplare deutlich über 20 PS. |
| Moderne Rakete: 19 Mio. kW (26
Mio. PS) |
| Deutsche Untertitel möglich . . .
|
Leistung (indiziert)
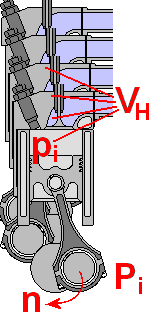
Während die effektive Leistung an der Kupplung gemessen werden kann, wird die indizierte Leistung (Innenleistung) durch den Innendruck berechnet. Der
mittlere Innendruck berücksichtigt dabei nur die Verluste
durch die drei vorbereitenden Takte. Andere Verluste, z.B. durch die Motorsteuerung, bleiben außen vor. Die indizierte Leistung gibt also die theoretisch
erzielbare Leistung unter Idealbedingungen an und ist deshalb
immer höher als die gemessene Leistung.
| Zweitakter | Viertakter |
VH · pi · n
Pi =

600.000 |
VH · pi · n
Pi = 
1.200.000 |
Pi · 600.000
VH = 
n · pi |
Pi · 1.200.000
VH = 
n · pi |
Pi · 600.000
pi = 
n · VH |
Pi · 1.200.000
pi = 
n · VH
|
Pi · 600.000
n = 
pi
· VH
| Pi · 1.200.000
n = 
pi
· VH
|
| VH | Hubraum (gesamt) | mm3, cm3, dm3 (Liter) |
| n | Drehzahl (Kurbelwelle) | 1/min |
| pi | Druck (mittlerer, indiziert) | bar, N/m2, Pa, hPa |
| Pi | Leistung (indiziert) | W, Nm/s |
Leistungsgewicht

Das Leistungsgewicht berechnet den Anteil des Gewichtes von Motoren/Fahrzeugen pro Kilowatt ihrer Motorleistung. Hier entscheidet sich, wie viel kg
jedes kW Leistung schleppen muss. Den von anderen
Vierrädern unerreichbaren Bestwert für das Leistungsgewicht hält die Formel-1 mit fast 0,15 kg/kW Motor- (Bild) und ca. 0,9 kg/kW Fahrzeug-
Leistungsgewicht. Hier die Daten für Serien-Motorräder (Leergewicht mit
vollem Tank):
| 2007 | Yamaha YZF-R1
| 1,59 kg/kW (1,17 kg/PS) |
| 2008 | Suzuki GSX-R 1000 | 1,56 kg/kW (1,15 kg/PS) |
| 2008 | Honda Fireblade | 1,52 kg/kW (1,12 kg/PS) |
| 2008 | Kawasaski Ninja ZX-10R | 1,51 kg/kW (1,11 kg/PS) |
| Motor | Fahrzeug |
mM
mPM = 
Pe |
mF
mPF = 
Pe |
| mM = Pe · mPM | mF = P
e · mPF |
mM
Pe = 
mPM |
mF
Pe = 
mPF |
| m | Masse, Gewicht | kg |
| Pe | Leistung (effektiv) | W, Nm/s |
| mp | Leistungsgewicht | kg(kW) |
Liefergrad
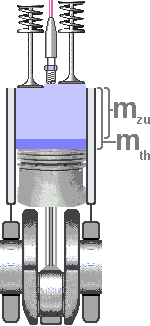
Der Liefergrad ist das Verhältnis von tatsächlich zugeführter Luftmasse zu der Luftmasse, die für eine vollständige Verbrennung nötig wäre.
mzu
λL
= 
mth |
mzu = mth · λL |
mzu
mth = 
λL |
| mzu | Zugeführte Luftmasse | kg |
| mth | Theoretisch benötigte Luftmasse | kg |
| λL | Liefergrad | |
Möglichkeiten zur
Verbesserung des Liefergrades
|
- Mehrventil-Technik
- Direkteinspritzung
- Aufladung durch besondere Saugrohrgestaltung
- Aufladung durch
Kompressor/Turbo/Ladeluftkühlung
- Innere Kühlung (Lachgas-,
Wassereinspritzung, fettes Gemisch) |
Luftverhältnis

| Mögliche Luftverhältnisse |
| Ideal (Benzin) | 1 |
| Kaltstart (Benzin) | ab 0,3 |
| Volllast (Benzin) | 0,85 - 1 |
| Diesel | > 1,3 |
Das Luftverhältnis ist das Verhältnis von tatsächlich zugeführter Luftmenge zu dem Luftbedarf bei einem idealen Mischungsverhältnis. Wenn in der
Aufgabe nicht anders angegeben, ist von einem theoretischen
Luftbedarf von 14,8 kg Luft je kg Kraftstoff (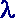 = 1) auszugehen. = 1) auszugehen.
| Lzu | Zugeführte Luftmasse je kg Kraftstoffverbrauch | kg |
| Lth | Theoretisch benötigte Luftmasse je kg Kraftstoffverbrauch | kg |
| λL | Luftverhältnis | |
Lufttrichter
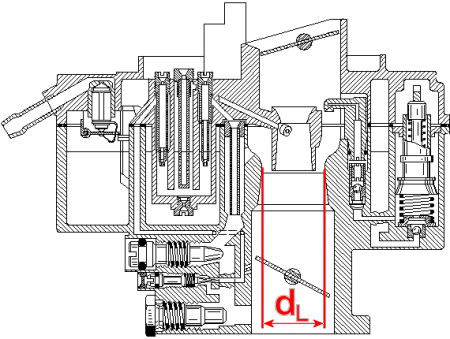
Es macht nicht viel Sinn, z.B. einen kleinvolumigen Motor mit einem zu großen Lufttrichter auszustatten. Deshalb ist es ratsam, den geeigneten
Durchmesser abhängig von Gesamthubraum, Zylinderzahl und
Maximaldrehzahl zu berechnen. Bitte beachten Sie, dass es sich hierbei um eine Faustformel handelt.
| VH | Gesamthubraum | dm3 (Liter) |
| nmax | Maximaldrehzahl | 1/min |
| z | Zylinderzahl | |
| dL | Durchmesser (Lufttrichter) | dm |
|
|