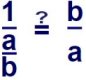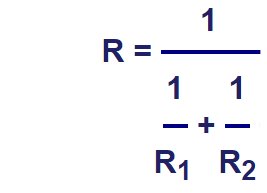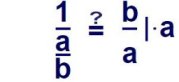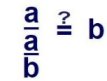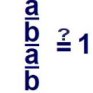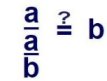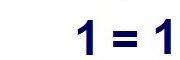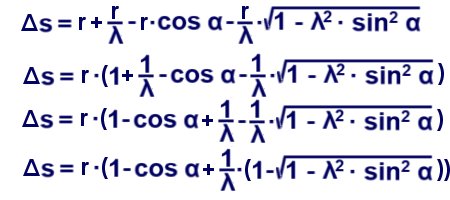
In Russland und Asien soll er nach Angaben des Brockhaus noch heute in Benutzung sein. Bei uns nur bis zum 15./16. Jahrhundert, der Abakus, die Rechenmaschine für die vier Grundrechenarten.
Vorwort
Prozent 1
Allgemein 1
Density
Formeln 1
Gleichungen 1
Gleichungen 2
Brüche 1
Brüche 2
Gleichungen 3
Brüche 3
Prozent 2
Brüche 4
Dreisatz 1
Dreisatz 2
Runden
Prozent 3
Prozent 4
Allgemein 2
Fehlentwicklungen 1
Fehlentwicklungen 2
Allgemein 3
Diagramme 1
Diagramme 2
Formeln 2
Diagramme 3
Diagramme 4
Diagramme 5
Diagramme 6
Diagramme 7
Diagramme 8
Funktionen 1
Funktionen 2
Formeln 3
Allgemein 4
Dreisatz 3
Fehlentwicklungen 3
Geometrie 1
Geometrie 2
Geometrie 3
Funktionen 3
Funktionen 4
Dreiecke 1
Dreiecke 2
Dreiecke 3
Dreiecke 4
Funktionen 5
Fehlentwicklungen 4
Allgemein 5
Geometrie 4
Zusammenfassung
Aufgaben
Lösungen
Sollte Ihnen das Buch gefallen haben, . . .
Alle gedruckten Bücher
Stichwortverzeichnis

Im Grunde ist die Baustelle oben ausreichend gesichert, wäre da nicht das Schild, auf das der schwarze Pfeil zeigt (Bild unten). Hier werden also Fußgänger aufgefordert, offensichtlich wegen der Baustelle die andere Straßenseite zu benutzen, obwohl die verpflichtende Fußgänger-Ampel sich dahinter befindet, Man kann also nur gegen das Schild oder die Regel verstoßen.
In diesem Fall eher verwirrend als hilfreich . . .

Auch wenn vielleicht jemand das Schild über Nacht umgedreht hat, so macht es auch dann wenig Sinn, weil man eigentlich ein von der Fahrbahn abgetrennter Fußgängerweg zur Verfügung steht und man andererseits über eine lange Wegstrecke nicht mehr auf die gewünschte Seite zurückkehren kann.
Zugegeben, das ist nur ein harmloses Beispiel für die einem fast überall ins Auge springende Unlogik unserer Zeit. Neben dem wohl auf mangelnder Überlegung beruhenden Fehlgriff in die Schilderkiste gibt es ja inzwischen auch jede Menge bewusst herbeigeführte Irritationen.
Schön, vielleicht mit diesem Buch für eine begrenzte Zeit in eine Welt mit verlässlichem Regelwerk abzutauchen, mit dem man später auch etwas in der Praxis anfangen kann, sei es beruflich oder privat. Unser Buch über die Chemie nimmt schon langsam Form an, hat im Prinzip schon eine Gliederung zumindest über die ersten 50 Seiten. Das über die Mathematik beginnt hier und jetzt, wird vermutlich zwei Jahre länger bis zur Fertigstellung brauchen.
Nein, es soll nicht zu schnell wachsen, wie ein Baum aus Buchenholz statt Birke, etwas darstellen, um in einem zweifellos schwierigen Feld Leute zu überzeugen, nicht zu überreden. Auch soll es nicht durch an den Haaren herbeigezogene Beispiele zu glänzen versuchen, an denen jede(r) merken kann, dass dahinter besonders Kniffliges versteckt ist.
Helfen soll allerdings der mögliche Bezug zur Kfz-Technik, zunächst vielleicht nur gefühlt. Was ist es doch toll, an einem Motor zu arbeiten, dessen Zylinderkopf ordentlich überholt und dessen Block vermessen und gerichtet wurde. Eine sichere Bank, auf der man aufbauen kann.
Läuft der Motor dennoch hinterher schleppend, so kann man sich beispielsweise bei der Fehlersuche auf die Hydrostößel stürzen und hat nicht ständig das Unbehagen evtl. tiefer sitzender Fehler.
Für mich hat Mathematik so etwas Ordnendes, etwas, was nicht jeden Tag anders ausgelegt werden kann, klare Kanten und Strukturen. Wer weiß, wo alles hingehört, tut sich leichter beim Aufräumen. Im Grunde hat das auch jedes Gebiet des Maschinenbaus. Manchmal erzählt jemand etwas und man weiß genau, so kann es nicht sein.
Schade, dass so viele Leute eine Gleichung, die nach einem längeren Rechengang endlich aufgeht, als nicht besonders befriedigend empfinden. Vielleicht braucht ja die Mathematik Geduld, die auch für andere Lebenslagen nicht so ungünstig wäre. Schrauben anziehen eben nicht nach dem Motto 'Fest, fester, abgerissen'.
Nein, nicht schnell hinter sich bringen. Im Gegenteil, sich dem Gegenstand langsam nähern. Erstmal den Text verstehen, möglichst sogar das Ergebnis vorher abschätzen. So soll eben auch das Buch entstehen. Gibt es keine vernünftige Idee für den Ein- bzw. Durchstieg im nächsten Kapitel, dann bleibt es halt noch eine Weile liegen.

So oder ähnlich könnte die Werbung ausgesehen haben, die Sie in positivem Sinn aufgeschreckt hat. Sie haben schon lange nach einem preiswerten neuen Auto Ausschau gehalten. Ihren alten haben Sie einem Verwandten versprochen.
Das Problem, Sie haben mit den 21,5 Prozent Rabatt im Freundeskreis angegeben und damit den Eindruck eines günstigen Kaufs erwecken wollen, bis einer im Kopf mal nachgerechnet hat.
Der hat sich die Zahlen ein wenig vereinfacht. Statt 19.990 Euro nahm er 20.000 Euro und statt 21,5 Prozent gut 20. Also zog er von 20.000 Euro ein gutes Fünftel ab und stellte fest, es hätten weniger als 16.000 Euro sein müssen. Das hat Ihrem Image als cleverer Einkäufer dann doch etwas geschadet.
Was tun? Natürlich wütend zum Händler und dort reklamiert. Der rechnet Ihnen vor, dass 21,5 Prozent von 16.453 Euro
16.453 Euro · 21,5 : 100 = 3.537 Euro
ergibt, was addiert zu 16.453 Euro zu exakt 19.990 Euro führt.
Bis jetzt hatten Sie gedacht, man könne sich auf die Mathematik verlassen. Aber wie kommt bitteschön die Differenz zustande? An der Mathematik liegt es nicht, sondern wieder einmal an deren Anwendung. Hier geht es hauptsächlich um die Frage, was man als Grundwert annimmt.

Geht man von 16.453 Euro aus, so landet man bei 19.990 Euro. Was aber wenn man von 19.990 Euro ausgeht? Da berechnen Sie ebenfalls zunächst die 21,5 Prozent:
19.990 Euro · 21,5 : 100 = 4.298 Euro
Von 19.990 Euro abgezogen ergeben sich jetzt 15.692 Euro. Sie hätten auch direkt mit (100 - 21,5 =) 78,5 Prozent malnehmen können. Ob der Händler Ihnen allerdings die 761 Euro Differenz auszahlt, daran haben wir so unsere Zweifel.
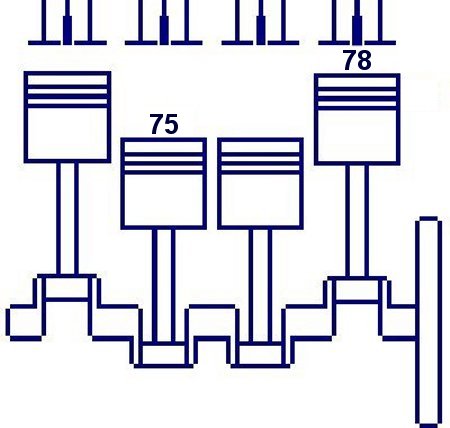
Wir arbeiten wir uns jetzt ein wenig durch obigen Motor . . .
Bohrung = 77 mm; Hub = 75 mm; z = 4; VH = 1.396 cm3
Schneller ist man einfach drauflos, tippt allerdings alles zwei Mal ein und vergleicht die Ergebnisse. Später werden wir noch eine bessere Überprüfung der Rechnung kennenlernen:
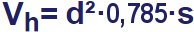
77 · 77 · 785 · 75 · 4 = 1.396.279,5
Dass der Motor oben mit vier Zylindern keine 0,13 cm3 hat, dürfte wohl klar sein. Könnte er denn 13.000 cm3 haben? Das wären dann 13 Liter Hubraum. Aber ein Lkw-Motor mit vier Zylindern hat so viel Gesamthubraum nicht. Außerdem ist es eher ein Benziner als ein Diesel, denn seine Bohrung ist größer als sein Hub.
Nenndrehzahl: 5.800/min; mittlerer Innendruck: 10 bar; Innere Leistung: 67,47 kW

1.396 · 5.800 · 10 : 1.200.000 = 67,4733333333333
Sie könnten sogar die Nullen und damit die '10' weglassen, das Ergebnis bliebe bis auf das Komma das gleiche. Denn der Motor wird doch weder eine Leistung von 6,7 noch 674 kW haben, oder?
Mechanischer Wirkungsgrad = 0,75; effektive Leistung = 50,6 kW (68,8 PS)
Max. Drehmoment in Nm bei 3000/min; effektive Leistung dabei = 30 kW
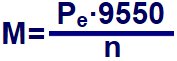
30 · 9.550 : 3.000 = 95,5
Hier könnte man besser eine echte Probe machen, statt alles zwei Mal einzutippen:
95,5 · 3.000 · 9.550 = 30
Kommen Sie wieder auf den Ursprungswert, war Ihre Rechnung in Ordnung.
E = m c2
|
Sogar der Punkt für die Multiplikation wird weggelassen.
|
Das englische 'Density' klingt etwas schöner als 'Verdichtung', aber genau das ist gemeint, ein großer Teil von Albert Einstein's Relativitätstheorie in diesem kurzen Ausdruck vereint. Auch steckt in dem c2 das Quadrat der Lichtgeschwindigkeit (300.000 km/s). Da muss schon ungeheuer viel Energie zusammenkommen, damit sich die Masse signifikant erhöht.
Vielleicht sind es ja die Buchstaben bzw. Formelzeichen, die von Mathematik bisweilen abschrecken. Übrigens ist die reine Schreibweise vielfach von Computerprogrammen ohne immer die exakte Deutung übernommen worden, anfangs noch mit ausgeschriebenen englischen Begriffen (Basic, Pascal), später mit stark abnehmender Tendenz. Nur die unmittelbare Gestaltung einer Internetseite ist relativ geschwätzig geblieben. Wird sie aber z.B. mit Javascript und PHP dynamisch, nimmt der Abstraktionsgrad zu.
Die Erkenntnisse vor der Abstraktion sind oft sehr banal, wie z.B. das jede auch nur mit einem Element gefüllte Menge mindestens ein kleinstes enthält. Das Problem dabei, wer sich auf diese Banalität verlässt, kann beim Übergang in die Abstraktion sehr schnell den Anschluss verlieren. Schon ein unbekanntes Zeichen in einer Gleichung kann ein Alleinstellungsmerkmal bedeuten, diesmal nicht positiv gemeint.
Deshalb soll in diesem Buch das Verständnis eines jeden Schrittes Vorrang haben. Hadern Sie nicht mit angeblich schwierigen Themen oder der Reihenfolge. Viel wichtiger ist es, dass Sie z.B. nach der Seite 50 und einem nicht allzu großen Zeitraum noch dabei sind.
| b · c |
| a = |  |
| d |
Was ist eine Formel und wozu braucht man sie? Man könnte sie auch als 'Rechenvorschrift' bezeichnen. Nimm den Wert, den Du in Variable b eingesetzt hast und multipliziere ihn mit dem Wert in Variable c. Teile das Ergebnis durch Variable d und weise dieses Ergebnis Variable a zu.
Es wird also für beliebig einzusetzende Zahlen eine genaue Vorgehensweise vorgeschrieben. Manche Schritte darf man vertauschen, wie z.B. erst b durch d zu teilen und dann mit c zu multiplizieren. Wären aber a und b durch ein Pluszeichen verbunden, dann müsste diese Berechnungsart zuerst durchgeführt werden.
| b + c |
| a = |  |
| d |
Warum? Ganz einfach, weil dann je nach Reihenfolge verschiedene Ergebnisse möglich wären. Wenn man nicht weiß, ob man etwas darf oder nicht, einfach mit den gleichen Zahlen beide Wege zu versuchen und schauen, ob die Ergebnisse übereinstimmen? Nicht sehr sinnvoll, denn die Ergebnisse könnten zufällig die gleichen sein und einen auf eine falsche Fährte führen.
Ist etwas in Ordnung, weil es ein, fünf oder gar zehn Mal funktioniert? In der Technik gibt man sich mit wesentlich mehr Versuchen viel Mühe. Seien Sie froh, dass einem die Mathematik so etwas erspart. Hier helfen Regeln, auch wenn sie häufig von Lernenden als sehr störend empfunden werden. Dazu ein Beispiel:
Früher habe ich mich beim Programmieren immer geärgert, wenn der Compiler, der aus einem Programmtext eine ausführbare Datei macht, noch dies und jenes zu meckern hatte und mich nicht zum Ziel kommen ließ. Programmiert man fürs Internet, dann gibt es keine Fehlermeldungen, allerdings auch keine Hinweise darauf, was man denn falsch gemacht hat.
b - c
a =
d
| b - c |
| a = |  |
| d |
Um dieses Kapitel nicht unbedingt fachfremd zu beenden, hier noch zwei kleine Definitionen:
Was hier oben sehen, ist eine Funktion. Sie ist bestimmt durch das Gleichheitszeichen, in diesem Fall in der Mitte. Dadurch ergeben sich eine linke und eine rechte Seite. Das wären aber jetzt keine mathematisch korrekten Bezeichnungen, sondern man nennt die Kombination von Variablen, Zahlen und Rechenzeichen ohne Gleichheitszeichen:
Term
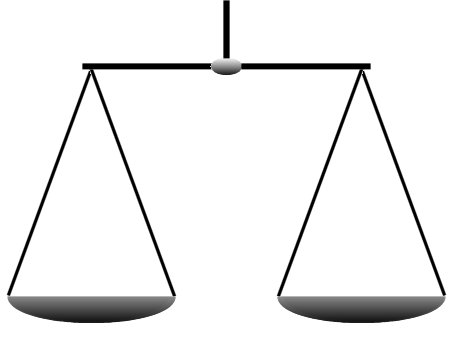
Der wichtigste Teil ist 'gleich' in dem Begriff 'Gleichung'. Natürlich ist eine Gleichung auch eine Formel, aber in der Regel eine, die z.B. zu einer anderen Variablen hin aufgelöst werden soll. Und genau deshalb soll das Gleichheitszeichen unbedingt beachtet werden. Als Symbol dafür ist die Waage oben abgebildet.
Die Gleichung wird bei allen Änderungen so angeordnet, dass das Gleichheitszeichen grundsätzlich in der Mitte ist, als besonders wichtiger Hinweis. Alle Veränderungen auf der einen Seite sind in gleicher Weise auch auf der anderen auszuführen. Nur dann bleiben beide Waagschalen auf gleicher Höhe.
| | b · c |
| a | = |
 | · d | · d |
| | d |
Rechts hinter dem senkrechten Strich steht das, was auf beiden Seiten zu tun ist, in diesem Fall d zu multiplizieren.
| | b · c · d |
| a · d | = |
 |
| | d |
Hier sehen Sie den ausgeführten Vorgang, wodurch sich d rechts wegkürzen lässt, was ja der Sinn der Übung war.
Jetzt stört rechts nur noch c. Hierzu ist immer das umgekehrte Rechenverfahren zu wählen, in diesem Fall Dividieren statt Multiplizieren.
| a · d | | b · c |
 | = |
 |
| c | | c |
Das ist das letzte Mal, dass dieser Schritt mit ausgedruckt wird. Schließlich kann man sich denken, dass durch Kürzen c nur noch auf der linken Seite erscheint.
| a · d | | |
 | = | b |
| c | | |
So könnte die Gleichung bleiben, denn jetzt kann b ausgerechnet werden. Nur der Schönheit zuliebe werden noch die Seiten vertauscht. Es ist eben wie bei einer Waage, wenn beide Seiten gleich sind, kann man sie auch tauschen.
| | a · d |
|
b | = |  |
| | c |

Wir haben die Waage dieses Mal noch beibehalten, zur Ermahnung sozusagen.
| | b + c |
| a | = |
 | · d | · d |
| | d |
Auf den ersten Blick liegt hier kein besonderer Fall vor und wir können genauso verfahren wie beim Produkt von b und c. Also d auf beiden Seiten multiplizieren und damit d auf die andere Seite bringen.
Jetzt stört rechts nur noch c. Hier wieder das umgekehrte Rechenverfahren, in diesem Fall Subtrahieren statt Addieren.
Wir verzichten ab jetzt auf die Schönheitsoperation, durch Seitentausch die gesuchte Größe unbedingt auf die linke Seite bringen zu wollen. Immerhin lässt sie sich auch so ausrechnen.
Was ist hier passiert? Hier stehen zwei völlig unnötige Klammern, denn nach den Regeln der Mathematik ist klar, dass Punkt- vor Strichrechnung geht. Wir haben sie trotzdem eingesetzt, um noch einmal daran zu erinnern und zu verhindern, dass zunächst c von d abgezogen und dann mit a multipliziert wird.
Jetzt haben wir nur den Zähler (alles oberhalb des Bruchstriches) mit dem Nenner (alles unterhalb des Bruchstriches) vertauscht und schon wird es ein ganzes Stück komplizierter. Denn ein Bruchstrich steht nicht nur für das Rechenzeichen ':' (Division), sondern hat zusätzlich die zusammenfassende Wirkung einer Klammer. Sie müssten sich also Zähler und Nenner jeweils als eingeklammert vorstellen.
Und so setzen wir schon jetzt 'c + d' in eine Klammer, damit dieser Teil der Gleichung auf der anderen Seite richtig ankommt.
Hätten wir die Klammer nicht gesetzt, so müssten jetzt a und c miteinander multipliziert und d addiert werden. Jetzt aber lautet die Rechenvorschrift, erst c und d zu addieren und dann mit a zu multiplizieren, ein wesentlicher Unterschied. Das Problem ist nun, abstrakt auf der Ebene der Variablen zu bleiben und trotzdem weiter zu kommen.
Hier haben wir ein Verfahren angewandt, das uns ein Weiterkommen ermöglicht, das 'Ausklammern'. Statt a mit der Summe von c und d zu multiplizieren, nehmen wir zunächst a mit c und dann a mit d mal und verbinden beide mit dem schon vorhandenen Pluszeichen. Das geht immer dann, wenn in der Klammer Variablen durch Strichrechnung, also auch ein Minuszeichen, miteinander verbunden sind. Logisch, denn bei Punktrechnung braucht man keine Klammern.
Besonders wichtig, dieses Verfahren ist reversibel, kann also auch umgekehrt angewandt werden. Taucht also bei jeder der Variablen in einer Strichrechnung die gleiche zu multiplizierende Variable auf, kann man sie jeweils herausnehmen, vor (oder hinter) eine Klammer und den Rest des Ausdrucks in die Klammer setzen.
Hoffentlich ist es jetzt klar, Variablen in Klammern oder solche, die durch Punktrechnung miteinander verbunden sind, müssen immer zuerst ausgerechnet werden. Man verstößt aber nicht gegen diese Regel, wenn man solche Ausdrücke bei der Übertragung auf die jeweils andere Seite zusammen lässt, so wie ganz oben bei der Übertragung der kompletten Klammer.
Der letzte Schritt, nämlich die Variable c auf die andere Seite zu bringen, dürfte keine Probleme mehr bereiten.
Besonders wichtig nach dem bisher Gesagten ist zu betonen, dass hier zunächst b mit d multipliziert und erst dann von b abgezogen werden muss.
Sollten Sie jetzt an dem Ergebnis stören, dass a sowohl im Zähler als auch im Nenner vorkommt, dann sei unten nur auf die berühmte Formel für das Verdichtungsverhältnis hingewiesen, in der VC ebenfalls im Zähler und im Nenner vorkommt.
Man könnte die Ergebnisgleichung auch etwas vorteilhafter schreiben, nämlich a und d näher aneinanderrücken. Dadurch würde man sie quasi als andere Variable als das a alleine wahrnehmen. Die Versuchung, hier etwas kürzen (siehe nächstes Kapitel) zu wollen, würde abnehmen.

Bei Brüchen ist unbedingt zu vermeiden, dass der Nenner Null wird. Das muss z.B. in einem Computerprogramm unbedingt ausgeschlossen werden, sonst besteht die Gefahr, dass es sich verabschiedet. Warum? Teilen Sie mal eine beliebige Zahl zunächst durch sich selbst, also mit dem Ergebnis 1. Jetzt verkleinern Sie die Zahl, durch die geteilt wird, also den Nenner. Dabei wird der Zähler immer größer, bis er unkontrollierbar gegen Unendlich strebt. Unkontrollierbare Bereiche hat man in der Mathematik nicht so gern, weil dann das Regelwerk nicht mehr greift.
a a · c
=
b b · c
Was sagt uns diese Gleichung? Hier sind Zähler und Nenner mit der gleichen Variablen (Zahl) multipliziert worden und siehe da, der Wert des Bruchs bleibt gleich. Viel beliebter ist allerdings die umgekehrte Methode, nämlich Zähler und Nenner durch die gleiche Zahl (Variable) zu teilen. 'Kürzen' nennt man das, was häufig überladene Brüche wieder etwas überschaubarer macht.
a · c a
=
b · c b
Vorsicht ist aber geboten, wenn die zu kürzende Variable im Zähler oder im Nenner zwei Mal auftaucht. Hier ist die Versuchung groß, sie im Nenner ein Mal und im Zähler gleich doppelt wegzustreichen.
ad · bd a · bd
=
cd c
Dann darf sie nur einmal gegen die im Nenner gekürzt werden, denn eigentlich steht im Zähler:
a · d · b · d
Ganz anders ist die Situation, wenn im Zähler eine Strich- statt der Punktrechnung vorliegt:
ad + bd a + b
=
cd c
Hier greift der alte Spruch: 'Summen kürzen nur die Dummen', der natürlich auch für Differenzen gilt. Und warum konnten wir hier trotzdem kürzen? Weil wir in Wirklichkeit zwei miteinander multiplizierte Termen (ein Produkt) gekürzt haben, denn hier lässt sich d ausklammern:
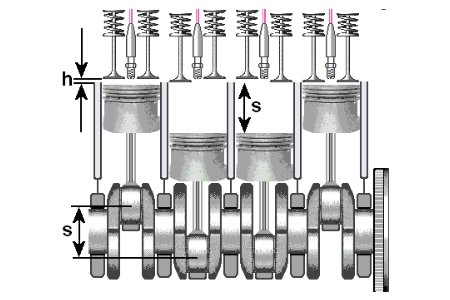
Vh + Vc
? = | · Vc
Vc
Das Ausklammern ist so wichtig, dass wir es an dieser Formel (Gleichung) noch einmal üben sollten. Beachten Sie hier bitte zusätzlich, dass die meisten ersten Transaktionen bei einer Formelumstellung dazu dienen, den Nenner zu eliminieren.
? · Vc = Vh + Vc | - Vc
Sie merken schon, wenn jetzt auch noch Vc auf die andere Seite muss, braut sich links etwas zusammen.
? Vc - Vc = Vh
Wir haben schon den Punkt zwischen ? und Vcweggelassen, damit Sie ja nicht auf die Idee kommen, Vc - Vc wegzunehmen. Aber jetzt wird es ernst. Auch wenn diese Formel für die Berechnung von Vhausreichen würde, sollten Sie noch den nächsten Schritt vornehmen:
Vc · (? - 1) = Vh
Sie werden sich fragen, wo denn plötzlich die '1' herkommt. Das ist eine Art Platzhalter für Vc. Besonders erfolgreich sind Sie nämlich beim Ausklammern, wenn Sie zur Probe die Klammer noch einmal aufzulösen versuchen, also 'einklammern'. Dazu sind dann nacheinander ? und die '1' mit Vc zu multiplizieren und dann beide so entstandene Terme durch Minuszeichen verbunden in die Klammer zu schreiben. Die '1' hat also den Sinn, dass auch die Probe erfolgreich ist.
Vc · (? - 1) = Vh | : (? - 1)
Zur Berechnung von Vh wären wir fertig gewesen. Die Auflösung der Gleichung nach Vh erforderte noch einen weiteren Schritt.
Vh
Vc =
? - 1
Sie sehen, die Klammern sind durch den Schutz des Bruchstrichs überflüssig geworden. Unsere Gleichung hat den Endzustand erreicht. Vielleicht ist Ihnen auch klar geworden, wie einfach und elegant Gleichungen durch die Technik des Ausklammerns bisweilen werden.
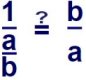
Sie sehen, man kann '1' oder auch eine beliebige Variable durch einen Bruch teilen. Wo kommt das in der Kfz-Technik vor? Z.B. wenn zwei verschiedene Widerstände parallel geschaltet sind und man den Gesamtwiderstand ausrechnen will:
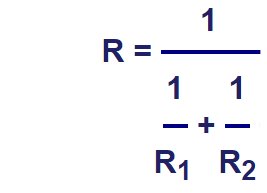
In dieser Gleichung wird behauptet, deshalb das Fragezeichen auf dem Gleichheitszeichen, das man statt durch einen Bruch zu teilen, auch mit ihm malnehmen kann, allerdings Zähler und Nenner vorher vertauschen muss (Kehrwert).
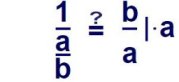
Jetzt benutzen wir also eine Gleichung zur Beweisführung, in der Mathematik relativ häufig. Trotzdem gehen wir wie gewohnt vor, indem wir versuchen, rechts den Nenner zu eliminieren.
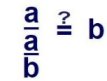
Ein Bruch wird mit einer Zahl bzw. Variablen multipliziert, indem man den Zähler mit der Zahl multipliziert. Das tun wir hier, schreiben aber statt 1 · a nur noch a in den Zähler links.
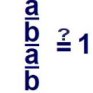
Und wenn wir mit dem Zähler multipliziert haben, dann können wir auch durch den Zähler teilen. So entsteht dann ein Bruch, der durch einen Bruch geteilt wird (Doppelbruch).
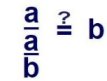
Und jetzt müsste wirklich einleuchten, dass man den mit dem Nenner identischen Zähler gegen diesen kürzen kann. Zwei gleiche Zahlen durcheinander dividiert ergeben immer 1.
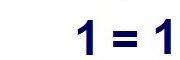
Der Beweis ist erbracht, weshalb das Fragezeichen verschwinden kann. Es gibt da eine lateinische Unterschrift:
Quod Errat Demonstrandum (was zu beweisen ist/war).
Regel: Durch einen Bruch wird geteilt, indem man mit dem Kehrwert multipliziert.

So ähnlich könnte die Rechnung über einen Autokauf aussehen. Entscheidend hier sind die Preise in Euro, genauer gesagt die Reihenfolge, in der das Skonto abgezogen und die Mehrwertsteuer hinzugefügt wurden. Könnte man diese auch tauschen? Bliebe das Ergebnis gleich?
Bevor Sie jetzt zu rechnen beginnen, hier ein kleiner Test (etwas Kopfrechnen gefragt):
Von 24 die Hälfte, dann ein Drittel, dann ein Viertel
Von 24 ein Drittel, dann ein Viertel, dann die Hälfte
Von 24 ein Viertel, dann die Hälfte, dann ein Drittel
Wenn Sie richtig gerechnet haben, kommt jedes Mal Eins heraus. Sie merken schon, es ist egal, in welcher Reihenfolge man multipliziert (oder dividiert), das Ergebnis ist stets dasselbe.
Und wie würde die Sache ausgehen, wenn das Skonto nur als feste Summe subtrahiert und nicht prozentual abgezogen würde?

Dann würde das Vertauschen der beiden Rechenverfahren zu dem Ergebnis 11.600,- führen und damit ungünstiger ausfallen. D.h. solange es sich ausschließlich um Strich- oder Punktrechnung handelt, kann man die Anwendung der Einzelrechnung vertauschen.
(a2)3 = (a3)2
Hier sehen Sie, dass dies sogar für Potenzen gilt, der nächsten Stufe in der Hierarchie von Rechenverfahren, denn es läuft immer auf
a · a · a · a · a · a
hinaus.
Zwei Brüche werden multipliziert, indem man jeweils die Zähler und die Nenner multipliziert. Anschließend können Sie die Rechenzeichen auch weglassen.
Wie aber ist die Situation bei einer Mischung der beiden Rechenarten? Wie fassen wir die beiden Brüche zusammen?
1 · b 1 · a a + b
+ =
a · b b · a a b
Man kann zwei Brüche nur addieren, wenn sie den gleichen Nenner haben. Das wird erreicht, indem man jeweils den einen Bruch mit dem Nenner des anderen Bruchs erweitert. Dieser gemeinsame Nenner wird dann 'Hauptnenner' genannt.
Vorteilhaft hier wieder, dass wir die beiden Elemente der Summe (Ergebnis einer Addition) im Zähler und die beiden Elemente der Produkte (Ergebnisse von Multiplikationen) jeweils vertauschen konnten.

Hier wird ein Hauptnenner für drei Summanden gesucht. Der soll also in allen drei Nennern durch Multiplikation gewonnen werden. Es ist '4ce', was im ersten Nenner durch '2c', im zweiten durch '4' und im dritten durch 'e' erreicht wird.
Nachdem die drei Brüche entsprechend erweitert sind, können Sie auf den gemeinsamen Nenner gebracht und alle Zähler ebenfalls zusammengefasst werden. Dabei ergibt sich hier zusätzlich die Möglichkeit, aus '4de' und 'de' durch Addition '5de' zu machen.

Sie haben ein kleines Problem. Sie brauchen knapp 4 Liter Motoröl, aber es werden nur Gebinde zu 2 und zu 4,5 Liter angeboten. Klar, werden Sie sagen, dann nehme ich 2 Mal die kleineren und habe meine 4 Liter.
Jetzt haben Sie aber die Erfahrung gemacht, dass größere Mengen pro Liter günstiger sind. Also doch 4,5 Liter nehmen und einen halben Liter zum Nachfüllen behalten? Unsinn, nach dem letzten Ölwechsel mussten Sie auch nicht nachfüllen. Also 4,5 Liter nur, wenn die pro Liter billiger sind.
Zur groben Abschätzung runden Sie grundsätzlich die für die Werbung günstiger gehaltenen Preise um die ein oder zwei Cent auf. Dann wird es auf einmal sehr einfach, denn Sie müssen nur die jetzt 16 Euro verdoppeln und sehen, dass zwei Gebinde je 2 Liter teurer als die 4,5 Liter wären.
Sie werden sagen, in diesem Beispiel funktioniere das gerade noch, aber im richtigen Leben sei es oft schwieriger. Recht haben Sie, also rechnen wir das einmal mit einem Verfahren, das in jedem Fall funktioniert:
Der erste Satz fasst immer die Gegebenheiten zusammen. Hier ist es wichtig, die später auszurechnende Größe nach hinten zu platzieren, in diesem Fall also den Preis. Der zweite Satz wird auch 'Einheitssatz' genannt. Er schließt grundsätzlich auf die 1. Wegen eventueller Möglichkeiten des Kürzens und auch der Ökonomie wird hier noch nicht ausgerechnet.
Ausnahme: Es wird nach der Menge 1 gefragt, man will also nicht den Preis für 4,5, sondern für 1 Liter Motoröl wissen.
In allen anderen Fällen schließt der dritte Satz dann auf die geforderte Menge, ergibt in diesem Fall also
35,96 Euro.
Klar, das war gar nicht die Frage. Sie wollten wissen, ob sich die 4,5 Liter auch dann lohnen, wenn Sie momentan nur 4 Liter davon brauchen. Dann nehmen Sie einfach den Preis von 4,5 Liter, setzen ihn 4 Litern gleich und schließen auf 2 Liter:
Das Ergebnis: 15,49 Euro.
Sie sparen also gegen jedes der beiden 2-Liter Gebinde 0,49 Euro = 0,98 Euro und haben am Ende noch einen halben Liter übrig.
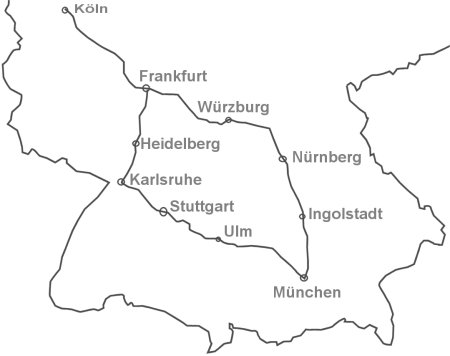
Wenn Sie einen der am meisten benutzten Routenplaner im Internet befragen, dann läuft deren Schätzung bei den meisten längeren Autobahnstrecken auf etwa 100 km/h hinaus. Und wer meint er/sie sei schneller, sollte es einmal wirklich auswerten, darf sogar die Pausen abziehen. Erstaunlich, wie stark sich der Mensch verschätzen kann. Obwohl, kommen genügend zusammen, dann schätzen Sie im Mittel z.B. das Gewicht eines Bullen aufs Kilogramm genau.
Die Aufgabe: Sie fahren von Köln nach München. Über Nürnberg und die A9 gibt der Routenplaner 574 km und 5 Std 40 Min an. Welche Zeit müsste er über Karlsruhe und die A8 bei 591 km angeben?
Am besten, Sie wandeln die 5 Std 40 Min in 340 Minuten um.
So, das war jetzt der übliche Dreisatz mit Division im zweiten Satz, in dem von der bekannten Vielheit auf die Einheit geschlossen wird. Im dritten Satz wird dann beim Schluss von der Einheit auf die noch unbekannte Vielheit malgenommen.
Heraus kommen 350 Minuten, also 10 Minuten mehr. Übrigens gibt der Routenplaner 32 Minuten mehr an, berücksichtigt also Verkehrslage und Baustellen.
Neue Aufgabe: Wir nehmen natürlich die kürzere und offensichtlich auch schnellere Strecke. Bei dem ganz oben angesprochenen Durchschnitt von 100 km/h würden wir 5,74 h brauchen. Bleiben wir für einen Moment bei der ungewöhnlichen Dezimalzahl. Es geht nämlich jetzt um die Frage, wie lange wir bei 110 km/h brauchen würden.
Hier hat sich im zweiten und dritten Satz die Logik ein wenig verändert. Es wird jetzt erst multipliziert und dann erst dividiert, typisch z.B. für Aufgaben, die mit dem Faktor 'Zeit' zusammenhängen.
Als Ergebnis notieren wir 5,22 Stunden.
Als Ergebnis erhalten wir 313 Minuten. Mit diesen Beispielen ausgerüstet, können Sie die Zeit bei 100 km/h leicht in Minuten umrechnen und erhalten als Differenz die reine theoretische Fahrzeitersparnis, etwas mehr als eine halbe Stunde.

Siegerauto: Le Mans Prototyp Porsche 919 Hybrid
Bei den 24 Stunden von Le Mans 2017 starten nach Audis Weggang nur noch fünf LMP1-Fahrzeuge, zwei von Porsche und drei von Toyota. Während des Rennens fallen 3 der Wagen komplett aus, zwei bleiben übrig, von denen der Toyota zwei und der Porsche eine Stunde lang repariert werden musste.
Jetzt wittern die LMP2 Morgenluft. Das ist eine Gruppe von fast gleichwertigen Fahrzeugen, allerdings mit weniger Leistung und neben Profis auch von Amateuren pilotiert. Aufs Podest kommt in jedem Fall eines von ihnen, obwohl es mit Rundenzeiten von 3:30 Minuten 10 Sekunden langsamer ist.
Schafft zumindest der Porsche 919 Hybrid noch den Gesamtsieg?
LMP2
Geg: t1 = 3:30 m = 210 s, tges = 24 h = 86.400 s
Ges: nRunden
Formel: nRunden = tges : t1
Rechnung: nRunden = 86.400 s : 210 s = 411,42
Ein Durchschnitts-LMP2 schafft mehr als 411 Runden.
Porsche LMP1 - eine Stunde Ausfall
Geg: t1 = 3:20 m = 200 s, tges = 23 h = 82.800 s
Ges: nRunden
Formel: nRunden = tges : t1
Rechnung: nRunden = 82.800 s : 200 s = 414
Der Porsche-LMP1 schafft 414 Runden.
Toyota LMP1 - zwei Stunden Ausfall
Geg: t1 = 3:20 m = 200 s, tges = 22 h = 79.200 s
Ges: nRunden
Formel: nRunden = tges : t1
Rechnung: nRunden = 79.200 s : 200 s = 396
Der Toyota-LMP1 schafft 396 Runden.
Können Sie der Kalkulation eine mögliche Ungenauigkeit ansehen? Sieht doch alles recht exakt aus, oder? Hat nur einen Haken, die Rundenzeit. Die ist als Mittelwert angenommen. Aber welches Fahrzeug wird schon ca. 400 Runden lang mit stets der gleichen Zeit betrieben.
Sicherlich, Kobayashi ist mit seinem Toyota in der Qualifikation mit knapp 3:15 m auf die Pole Position gefahren. Aber schon Bernhard hat mit dem späteren Sieger-Porsche über 1:17 m gebraucht. Solcherart schnellste Runden werden im Rennen eher selten erreicht. Und während der Nacht müssen Sie dann noch 2 bis 3 Sekunden addieren.
Dabei ist der Spielraum gering. Ist der Porsche im Mittel nur eine Sekunde langsamer, kommt er auf die gleiche Rundenzahl wie LMP2. Deshalb kann eine sehr exakte Rechnung mit noch so vielen Stellen hinter dem Komma stets nur so gut sein, wie es die Eingabewerte vorgeben.
Und dann sind da noch die Rundungsfehler. Hätten wir alle Zeiten in Minuten statt in Sekunden umgewandelt, wären Rundungen unvermeidlich geblieben. Gute Taschenrechner geben deshalb Zwischenergebnisse, wenn nicht anders eingestellt, als Brüche aus und berechnen erst am Ende einen Dezimalwert. Dadurch sind Rundungsfehler nur einmal in der Rechnung enthalten.

Was haben Prozent, also Anteile von 100, mit einem Alkoholtest (oben im Bild) zu tun? Wenn wir statt auf 100 Anteile auf deren 1.000 beziehen, werden Sie sofort verstehen, dann sind es nämlich Promille.
Lateinischer Ursprung
pro für
centum hundert
mille tausend
Vermutlich kennen Sie die berühmte 'Mille Miglia', das Rennen in Italien über 1000 Meilen, das heute nur noch mit historischen Fahrzeugen bestritten wird. Hier bedeutet es, man zerlegt einen Grundwert in hundert bzw. tausend Teile und multipliziert dann mit dem Prozent- bzw. Promillesatz.
Beispiel gefällig? Wenn wir eine Flasche Wein mit meist 0,75 Liter Inhalt betrachten und 13 Prozent Alkoholgehalt annehmen, können wir die enthaltene Alkoholmenge berechnen:
Das wären dann 0,0975 Liter, die wir großzügig auf 0,1 Liter aufrunden. Und jetzt ist die Frage, wie viel Promille ergäbe das, wenn der ganze Alkohol ins Blut übergehen würde. Wir gehen vom für den Alkoholgenuss günstigsten Fall aus, ca. 7 Liter Blut.
Es ergeben sich 1,43 Promille.

Wir haben inzwischen über 11.000 Aufgaben auf unseren Seiten. Diese werden als 'programmiert' bezeichnet, was meint, dass immer eine oder mehrere Lösungen vorhanden sind. Es gibt also in jedem Fall ein rechnerisches Ergebnis. Der neuste Gag ist die Anzeige wie bei Tacho und Drehzahlmesser, also doch noch altmodische Zeigerinstrumente, kein Display.
Bei solchen Instrumenten kommt es darauf an, möglichst die komplette Skala zu nutzen, was in beiden Fällen wohl gelungen ist. Relativ einfach, abgesehen von der Grafik, ist das linke Instrument. Hier hat man für jede Aufgabe eine Zeigerstellung und die entsprechende Schrift in dem kleinen Display, also exakt 20 Bilder, die man je nach Nummer der Aufgabe austauscht.
Schon etwas schwieriger war die rechte Skala, die eigentlich wichtigere, weil die bisherige Leistung anzeigend. Hier bedurfte es 21 Bildern, denn die 6,0 wird zu Beginn angezeigt und kann durchaus bei besonderer Fehlleistung auch wieder vorkommen. Bei der linken Grafik kann man sich die Zeigerstellung Null sparen, weil direkt mit der Aufgabe 1 begonnen wird.
Die richtige Grafik rechts wird berechnet, indem man pro Aufgabe z.B. maximal eine ganzen Punkt vergibt und bei Teillösungen entsprechend weniger. Wir gehen allerdings den Weg, nicht weniger als halbe Punkte zu verteilen. Nach alter Wertung entspricht das einer nicht gelösten Aufgabe. So, und jetzt muss man die nur noch durch die Anzahl der bisher bearbeiteten Aufgaben teilen.
Womit wir wieder bei der Prozentrechnung gelandet sind. Wenn Sie allerdings auf das Gesamtergebnis über jeder Aufgabe schauen, dann werden nach der ersten von 20 Aufgaben höchstens 5 Prozent ausgewiesen. Das hat pädagogische Gründe. Springt nämlich die Prozentzahl nach der ersten korrekt gelösten Aufgabe direkt auf '100', kann man sich eigentlich nur noch verschlechtern.
Das ist das Warten, bis unweigerlich der Sprung auf eine geringere Prozentzahl kommt. Die 100 Prozent können danach nie wieder erreicht werden. Da erscheint es dann pädagogisch sinnvoller bei einer kleinen Prozentzahl zu beginnen, die nie mehr unterschritten werden kann. Rein rechnerisch bezieht (teilt) man die erreichten Punkte also nicht durch die Zahl der bisher bearbeiteten, sondern aller vorhandenen Aufgaben.
Gibt man natürlich Noten wie oben beim Klick auf die Prozente des Gesamtergebnisses oder jetzt darunter in der rechten Uhr, dann ist es wiederum ungünstig, mit einen 'ungenügend' zu beginnen. Da bei letzterer außer der Null 20 Zeigerstellen vorhanden sind, braucht man hier die entsprechende Prozentzahl nur durch '20' zu dividieren. Allerdings musste beim Programmieren darauf geachtet werden, dass die Anzeige sofort nach dem Klick auf 'Bewerten' verändert wird, nicht erst, wie bei der linken, beim Wechsel zur nächsten Aufgabe.
Noch ein kleiner Tipp: Für Klassenarbeiten sind die Tests nicht geeignet, denn es wird für jede Aufgabe eine neue Seite aufgerufen. Die bis dahin erzielten Ergebnisse wären dann verloren, könnten auch nicht mehr angezeigt werden. Und da wir nicht mit Cookies arbeiten wollten, hängen wir die Ergebnisse an den Aufruf der nächsten Seite. Da diese Zahlen leicht veränderbar sind, kann man sich hier ein auch ein Traumergebnis einstellen.

Mit den negativen Zahlen, oben kombiniert mit einer Temperaturskala, erweitert sich das Spektrum zum ersten Mal. wir erhalten im Prinzip ebenso viele Zahlen, wie wir schon haben dazu. Dabei ist das Minuszeichen wohl eher richtunggebend als fest zu verorten.
Beispiel gefällig? Stellen Sie sich vor, vor einer Variablen steht ein Minuszeichen. Dann ist es gut, sich virtuell umzudrehen und in Richtung Minus zu blicken. Egal, was für einen Wert die Variable hat, es ist die Vorgabe. Steht die Variable samt ihrem Vorzeichen in Klammern mit noch einem Miinuszeichen davor, so muss man sich wieder umdrehen, also neu orientieren.
Plus mal Minus ergibt Minus.
Minus mal Minus ergibt Plus.
So ergibt sich ein grundlegender Unterschied zwischen Plus- und Minusklammer. Erstere macht nur Sinn, um z.B. Strich- vor Punktrechnung zu schützen. Die Minusklammer dreht zusätzlich die Vorzeichen aller Variablen in der Klammer um.
Plus durch Minus ergibt Minus.
Minus durch Minus ergibt Plus.
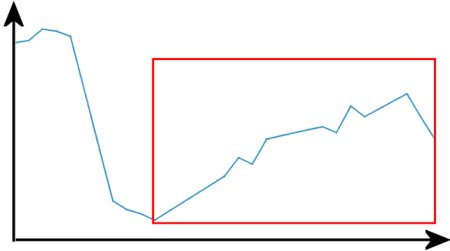
'Traue keiner Statistik, die du nicht selbst gefälscht hast.' Dieses Zitat wird Winston Churchill zugeschrieben, egal. Oben sehen Sie das erste Beispiel. Das soll die Entwicklung des DAX in einem bestimmten Zeitraum darstellen und genau auf diesen kommt es an. Wählt man ihn ganz, so entsteht der Eindruck, der sei insgesamt deutlich gefallen. Nimmt man hingegen nur den im Rechteck sichtbaren Teil, so meint man, er sei sehr stark gestiegen. Man könnte es auf die Spitze treiben und sogar noch den letzten Abfall weglassen.
Fast ebenso berühmt ist, das Beispiel aus Schweden, wo erstaunlicherweise die Geburtenrate immer zu einer Zeit stark anstieg, wenn die Storche aus dem Süden zurückkehrten. Hieraus lernt man, dass nicht jedes zeitliche Zusammentreffen auch einen kausalen Zusammenhang bedeutet.
Wenn Sie die Karten Europas und Afrikas nacheinander anschauen, würden Sie das (wiedervereinte) Deutschland auf nur gut ein Prozent der Fläche von Afrika schätzen? Hätte man Sie vorher gefragt, Ihre Schätzung wäre mit Sicherheit höher ausgefallen.
Da kann sich ein Ort oder gar ein Dorf durch Verkauf eines geeigneten Baugrundstücks an eine(n) Milliardär(in) recht schnell den Nimbus von Wohlhabenheit verschaffen, weil mit einem Schlag der Schnitt enorm angehoben wird. Berechnet jemand jetzt auch noch aus diesem Durchschnittswert den Prozentsatz der Armen mit der Grenze 60 Prozent von diesem Wert, so sinkt die Rate der Armen mit einem Schlag rapide. Obwohl keiner der vorher als arm 'Bezeichneten' auch nur einen Cent mehr hat.
Nach Meinung der Wissenschaft kann man eine Quote von Armut nur bestimmen, indem man in sehr vielen Lebensbereichen festlegt, was zum Leben unbedingt nötig ist. Und diese Kriterien müsste man zusätzlich auch noch offenlegen. Erst dann kann von außen eine solche Quote sinnvoll überprüft und natürlich auch angezweifelt werden.
So wird die Statistik und damit die Mathematik für Interessen missbraucht. Wir wollen das Thema hier gar nicht auf die zweifelhaften Methoden bei Fragebögen ausweiten. Ist doch klar, dass z.B. die Gewerkschaft dem Verstoß gegen 'Gleicher Lohn für gleiche Arbeit' besonders für Frauen eher eine höhere Quote und die Arbeitgeberverbände eher eine niedrigere zuordnen möchten.
Fragt man die Leute, ob Sie Bio-Kost bevorzugen, sagen sicher mehr 'Ja' als eine solche für teureres Geld wirklich kaufen. Sicher sind vielen Menschen dafür, die Autos aus der Stadt etwas mehr zu verbannen, aber vermutlich eher nicht aus der eigenen, in die sie täglich Einkaufen fahren.
Die Zahl der Leute, die sich durch entsprechende Statistiken bestimmten Gruppen von (besonders psychisch) Kranken zurechnen, ist so groß geworden, dass führende Therapeuten in der Regel grundsätzlich von einem/r gesunden Klienten/in ausgehen und sehr häufig auch dahingehend beraten.
Da wird dann im Fernsehen ein südkoreanischer Jugendlicher gezeigt zusammen mit der Nennung sehr hoher Zeitanteile, die dieser und seine Generation spielend vor dem Computer verbringt. Anschließend sieht man ihn bei einer genaueren Untersuchung, die dann zwar von einer 'Gefährdung', aber nicht von einer 'Sucht' spricht.
Mit dem Vergleich in Prozent lässt sich besonders viel Schindluder treiben. Dazu brauchen wir noch nicht einmal ein spezielles Beispiel. Wird ein Experiment durchgeführt, dann ist es üblich, dass mit der einen Hälfte der Leute etwas passiert und mit der anderen Hälfte nicht. Zeigen nun nach einer definierten Zeit sagen wir vier Personen der behandelten und zwei der Kontrollgruppe bestimmte Symptome, dann ist gleich von 50 Prozent 'Zuwachs' die Rede, egal ob es sich insgesamt um 10, 100, 1.000, 10.000 oder gar noch mehr Personen handelt.
Mögliche Probleme bei der Vorbereitung
1. Interessenkollision zwischen Fragenden und Fragen?
2. Ist Unehrlichkeit bei den Antworten zu erwarten?
3. Ist die Auswahl der Befragten richtig getroffen?
4. Ist die Zahl der Befragten ausreichend bemessen?
Mögliche Probleme bei der Auswertung
1. Vergleichs- oder absolute Zahlen?
2. Ist die Zeitachse unplausibel beschnitten?
3. Ist die ganze y-Achse oder nur ein Teil davon zu sehen?
4. Wird die Aussage der Darstellung den Zahlen gerecht?
5. Sind die zugrunde liegenden Definitionen erklärt?
6. Wird auf Kausalität oder nur auf Plausibilität gesetzt?

Autotests gibt es viele, da wundert man sich nicht mehr. Auch nicht darüber, dass die Autos in sehr fernen Ländern getestet werden. Was man nicht sieht, dass die Reise- und Unterbringungskosten meist komplett von den Autowerken bezahlt werden.
Soll das nachher im youtube-Kanal gesendet werden, ist natürlich auch jemand dabei, der die Kamera bedient. In Ausnahmefällen stellt sogar der Hersteller den/die Kameramann/frau. Fürs Fernsehen kann das Team noch größer sein, wird dann zumindest um eine(n) Toningenieur/in erweitert.
Nein, um diese Zumutung eines keineswegs unabhängigen Journalismus soll es uns hier nicht gehen. Auch nicht um die Spitzenleistung an Hirnriss, wenn ein 500 PS starkes Kompaktauto samt Fernsehteam in den Oman verfrachtet wird, wo es keinerlei Möglichkeiten eines auch nur annähernd realistischen Tests gibt und in der Regel Gefängnis bei Verkehrsübertretungen droht.
Den schnellsten Wagen zum Test in das mit am stärksten geschwindigkeitskontrollierte Land der Welt.
Nein, uns geht es um die, sagen wir einmal Umfahrung der Mathematik und einer vernünftigen Logik kombiniert mit offensichtlich noch massiverer Beeinflussung durch Hersteller. Hier ein besonders drastisches Beispiel des Missbrauchs journalistischen Handelns:
Der Fernsehbericht beginnt vergleichsweise harmlos. Es ist Frühjahr 2017 und man will einen Smart forfour mit einem BMW i3 vergleichen, zwei reine Elektroautos also. Erstes Misstrauen kommt auf, als der Ort des Tests genannt wird, nämlich Toulouse. Moment mal, ist dort nicht vor kurzem der neue Smart vorgestellt worden, sehr vermutlich auf Kosten von Daimler?
Aber gut, kein Grund zur Panik, geht es doch im Test zunächst um den Gepäckraum. Wie zu erwarten, gewinnt der i3. Als Gegengewicht wird ein zwei Meter großer Redakteur hinten in einen Smart gequetscht. Man sieht, es geht. Der Vergleich zum BMW fehlt. Noch immer schöpft man keinen Verdacht.
Es folgt dann doch etwas Unangenehmes, nämlich nur ein Satz, mal eben so hingeworfen: Der Smart sei gut für 160 km, der BMW für 190 km. Nur ein Satz, während sonst alles akribisch gezeigt und besprochen wird. Moment mal, Hat nicht der i3 gerade eine neue, den Radius deutlich erweiternde Batterie erhalten und der Smart ist trotz Neuauflage bei seiner alten Kapazität geblieben? Wie passt das zusammen?
Smart selbst gibt sogar nur 155 km an.
Die haben offensichtlich einen alten i3 zu der Vorstellung des elektrischen Smart in Toulouse hinzugenommen. Aber halt, selbst der alte i3 hat brutto 22 kWh Batteriekapazität, der neue Smart nur 17,6 kWh.
Geht mal also von der Bruttokapazität aus, was man bei der normalen Berechnung der Reichweite nicht tun sollte, aber bei einem Vergleich durchaus, dann kommt hier der Smart etwas zu optimistisch weg. Die einzig mögliche Lösung wäre, dass der Smart vielleicht weniger verbraucht. Wie gesagt, außer diesen fragwürdigen Angaben der Reichweite kein weiteres Wort zu diesem Thema.
Zum Test der Motorleistung fährt man durch die Stadt. Ist ja auch sinnvoll, denn über Land würde der Smart forfour mit 60 kW (81 PS) und 160 Nm auch gegen den alten i3 mit 125 kW (170 PS) und 250 Nm deutlich verlieren. Nein, in der Stadt bringt eine solche Mehrleistung keinen Vorteil. Und Stadtautos fahren ja bekanntlich nur in der Stadt!?
Es wird der tolle Wendekreis des Smart gezeigt und dann kommt der Film langsam zu seinem Fazit. Sicher der Verbrauch des Smart lag trotz etwa gleichen Gewichts bei ca. 18 kW/100km, während der BMW nur 15 kW/km verbrauchte, aber angesichts des riesigen Preisunterschieds empfiehlt man den Smart.
Dabei hätte jetzt der Unterschied in der Reichweite unbedingt korrigiert werden müssen. Schon die 0,06 von 1,19 bedeuten schon 5 Prozent Vorteil. Kommt der geringere Verbrauch hinzu, ergibt sich folgendes Bild:
Eine Variable/Zahl wird durch einen Bruch geteilt, indem man sie mit dessen Nenner multipliziert und durch dessen Zähler teilt.
Da wären dann aus 5 Prozent Vorteil 50 Prozent geworden, wohlgemerkt beim Vergleich mit einem Auto, das gerade durch eine in der Reichweite um 50 Prozent erweiterte Version ersetzt wird. Hier darf man ausnahmsweise die beiden Prozentzahlen addieren. Das hätte also knapp 100 Prozent mehr Reichweite erzielt.
Daimler braucht die Tester(innen) gar nicht explizit zu bestechen. Deren vorauseilender Gehorsam verbietet einfach Kritik an dem Konzern. Beispiel: Ein paar Wochen später erscheint ein Bericht über tatsächliche Abgaswerte. Die sind bei Audi, BMW und Mercedes gut und bei Renault und Nissan erwartungsgemäß sehr schlecht.
Natürlich haben die drei Deutschen als Oberklasse-Modelle ein SCR-System an Bord, während die Ausländer mit den viel kleineren Motoren nur über Speicherkats verfügen. Dass es aber auch z.B. eine A-Klasse von Mercedes mit diesen Motoren von Renault gibt, verschweigt der kurze Bericht. Und getestet wird diese Kombination schon gar nicht.

Zwei Hierarchiestufen haben wir kennengelernt, die Strich- und die Punktrechnung. Dabei stellt die Multiplikation als Punktrechnung eine Verkürzung der Addition dar:
Jetzt kommt das Rechnen mit Potenzen und Wurzeln hinzu, eine noch höhere Hierarchiestufe. Man könnte die Potenz wiederum als verkürzte Schreibweise der Multiplikation ansehen:
Am besten klären wir kleinere Potenzen als 2 direkt:
a1 = a
a0 = 1
Und wie geht das jetzt weiter?
Hier kommt wieder ein Mix aus Potenzen und anderen Rechenarten:
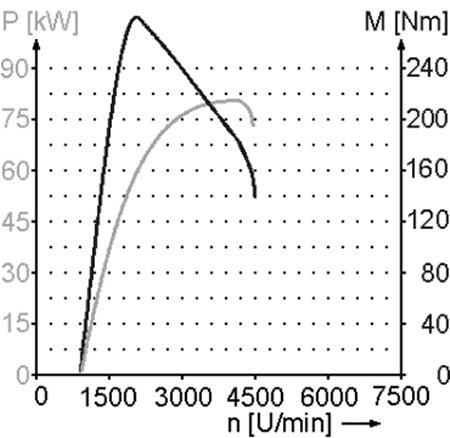
Ohne die Technik der Diagramme könnte man viele Sachverhalte in der Kfz-Technik gar nicht so einfach ausdrücken. Eigentlich sind in so einem Diagramm unendlich viele Werte vereint. Natürlich hat man sich z.B. am Prüfstand, wo die Werte oben entstanden sind, auf einige sogenannte Stützstellen beschränkt.
Ungewohnt, wenn man schon einige solcher Diagrammkombinationen gesehen hat, ist, dass die Drehmomentkurve teilweise über der Leistungskurve liegt. Aber mathematisch ist das alles völlig in Ordnung, solange die Achsen korrekt beschriftet sind und eine eindeutige Zuordnung einzelner Punkte auf der jeweiligen Kurve zu der Drehzahl auf der x-Achse und der Leistung bzw. dem Drehmoment auf der y-Achse besteht.
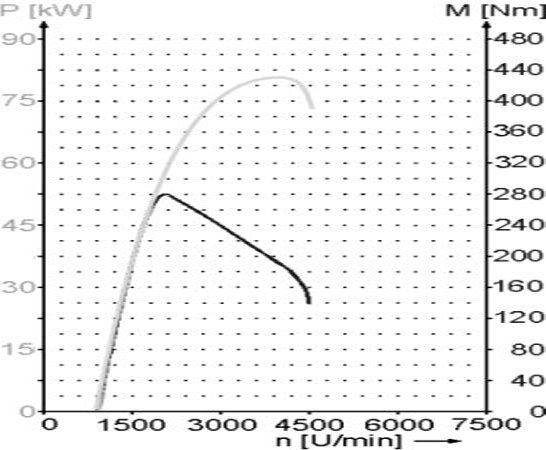
Um an diesem Beispiel einmal zu zeigen, wie sehr man solche Diagramme verändern kann, haben wir jetzt die Leistung in der Auflösung verdoppelt und die für das Drehmoment beibehalten. Ab jetzt liegt also die Leistungskurve über der des Drehmoments. Leider verdeckt sie diese in großen Teilen, weshalb das erste Diagramm eigentlich doch das etwas günstigere war.
Aber auch hier wäre Abhilfe möglich. Man müsste nur die Auflösung der Drehzahl deutlich erhöhen. Und wenn das nicht reicht, die beiden Kurven zu trennen, nimmt man eben nur den Bereich bis 4500/min und streckt diesen noch einmal, immerhin nutzt dieser Dieselmotor ja bei weitem nicht das gesamte Drehzahl-Spektrum. Sogar unten herum ließen sich noch mindestens 500/min abknapsen.
An diesem kleinen Beispiel mögen Sie die Möglichkeiten von Diagrammen erahnen. Bei gleichem x-Bereich lassen sich zwei (und vielleicht noch mehr) Kurven übereinander legen und anschaulich vergleichen. Wie mir einer Lupe lässt sich der entscheidende Bereich vergrößern. Allerdings muss man darauf achten, welchen Abstand die Stützstellen haben, also die wirklich gemessenen.
Wären auf dem gewählten Ausschnitt nur noch zwei vorhanden, würde man die dazwischen liegende, durch Interpolation gewonnene Linie interpretieren. Aber ansonsten lässt die Mathematik hier viel Freiraum und ist sogar noch richtig anschaulich. Fast genügt ein Blick, um die Zusammenhänge zu erfassen, was bei Kolonnen von Zahlen mit Sicherheit nicht so einfach wäre.
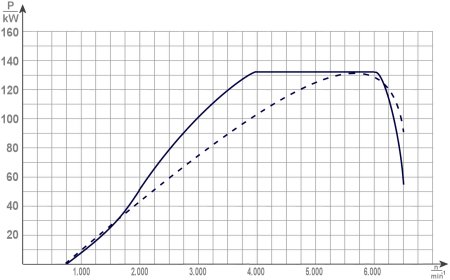
Während früher die Leistung eher der gestrichelten Linie gefolgt ist, sieht heute eine solche Kurve eher wie die durchgezogene aus. 'Schuld' ist die beinahe flächendeckende Einführung des Turboladers. Wer die Kurve zu interpretieren weiß, sieht es ihr gewiss an. Typisch, der horizontale Verlauf im Bereich der Spitzenleistung. Die Lader sind für den jeweiligen Motor etwas zu stark (nicht unbedingt groß) dimensioniert, müssen dann aber beim Erreichen eines gewissen Drucks abgeregelt werden.
FSo entsteht also die maximale Leistung über einen weiten Drehzahlbereich. Auch am Beginn der Kurve links kann man die Wirkung des Turboladers erahnen. Der hat bis ca. 2.000/min noch Schwierigkeiten den Motor mit ausreichend Luft (wegen des Turbolochs) zu versorgen, weshalb dieser im Vergleich zu einem gleich leistungsstarken Saugmotor leicht schwächelt. Allerdings können Sie bei diesem von deutlich mehr nötigem Hubraum ausgehen, während die durchgehende Linie mit zwei Liter Hubraum (2017) erreicht wird.
Jetzt sind wir also endgültig in der Praxis angekommen. Trotzdem gibt es bei solchen Diagrammen einiges zu beachten. Die Einheiten können Sie wählen, wie Sie wollen, auch gern unterschiedlich für y-Achse (Leistung) und x-Achse (Drehzahl). So kann ein Leistungsdiagramm je nach Auflösung in Breite und Höhe unterschiedlich ausfallen. Sie können auch gern ungenutzten Raum links und rechts weglassen. Wichtig ist, dass die immer gleichen Kreuzungspunkte durchlaufen werden, also jedem Drehzahlwert der korrekte Leistungswert zugeordnet ist.
Auch die Beschriftung der Achse ist nicht beliebig. Es hält sich zwar nicht jeder dran, aber eigentlich gehört an das Ende einer Achse ein waagerechter Strich, darüber die Kurzbezeichnung für die physikalische Größe, darunter die für die Einheit. Bei der Drehzahl ist es besonders kompliziert. Am Diagramm sieht sie so wie oben aus, im Text würde man z.B. 6.000/min (ohne Leerzeichen) schreiben.
Im Kapitel Funktionen 1 weiter unten sind sogenannte 'Funktionsgraphen' zu sehen. Sie entstehen aus einer Formel, die eine kontinuierlich verlaufende Linie erzeugt. Hier hingegen entsteht die Linie durch die Verbindung einzelner Messpunkte. Das ergibt oben bei der Leistung zwar eine Linie ohne Unterbrechung, aber das ist nicht immer der Fall. Übrigens handelt es sich wie oben meist um geglättete Linien. Der echt von den Prüfstandswerten stammende Verlauf ist in der Regel wesentlich unruhiger.
2·?·rdyn·nA·60
v =
1000
In der Kfz-Technik gibt es immer wieder dringend nötige Zuordnungen. Mehr noch als in der allgemeinen Physik haben sich Konstante eingebürgert, die eigentlich nur die Umrechnung der Einheiten ersparen. Oben sehen Sie ein Beispiel dazu.
Durch die '60' kann man die Drehzahl in der nur für diese Gleichung festgelegten Einheit min-1 eingeben und erhält die Fahrgeschwindigkeit in km/h. Die '1000' lässt die Eingabe des Radius 'rdyn' in 'm' zu, obwohl die Fahrgeschwindigkeit in km/h herauskommt. Die Formel bzw. Funktion hätte aber auch ohne diese Konstanten Bestand.
Die aus der Physik bekannten Konstanten dürfen hingegen nicht fehlen. Wie sollte eine Kreisflächen- oder Umfangsberechnung ohne die Kreiszahl ? möglich sein. Egal welche Art der Konstante vorliegt, für uns sind es feste Größen, die sich nicht ändern.
Ganz im Gegensatz dazu die Variablen. So kann in der Formel oben ein anderer Radhalbmesser und/oder eine andere Raddrehzahl eingesetzt werden. Also wäre eine der beiden Beziehungen in der Formel, z.B. die der Raddrehzahl zur Fahrgeschwindigkeit:
v(n)
Es gibt bei den Raddrehzahlen einen bestimmten Definitionsbereich, der z.B. negative Zahlen ausschließt. Und eine Zahl dieses Definitionsbereichs wird dem sogenannten Wertebereich zugeordnet. Halten wir den Raddurchmesser einmal konstant, dann könnten 500 Radumdrehungen pro Minute z.B. 110 km/h ergeben.
Logisch, dass dann 10 Prozent weniger Raddrehzahl auch 10 Prozent weniger Fahrgeschwindigkeit ergibt. Einer bestimmten Raddrehzahl muss immer einer ebenso bestimmte Fahrgeschwindigkeit zugeordnet werden. Auch der jeweilige Raddurchmesser gehört zum Definitionsbereich. Würde ich den gleichzeitig um 10 Prozent erhöhen, käme wieder die Fahrgeschwindigkeit von 110 km/h heraus.
Einer oder der Kombination mehrerer Variablen aus dem Wertebereich muss man immer eine einzige Größe des Wertebereichs zuordnen können, dann spricht man von einem funktionalen Zusammenhang oder einer Funktion. Was nicht geht ist, dass ein bestimmter Raddurchmesser und eine bestimmte Raddrehzahl zwei oder mehr Funktionswerte ergeben. Das ist zwar mathematisch möglich (y = ±x), macht aber für unser Anwendungsgebiet keinen Sinn.
1000
rdyn =
2 · ? · v · nA · 60
Was wohl geht, ist die Umkehrung der Abhängigkeit. Hierzu könnte man sich vorstellen, dass exakt der Raddurchmesser gesucht wird, der bei einer bestimmten Raddrehzahl eine ebenso bestimmte Fahrgeschwindigkeit ergibt. Dazu korrigiert man zwar eher die Übersetzungen im Antriebsstrang, aber für evtl. Feintuning oder eine Kontrollrechnung ist so etwas denkbar.
Was da geschehen ist, nennen wir die Vertauschung der unabhängigen und der abhängigen Variable. Unabhängig war zuvor der Radhalbmesser, abhängig die Fahrgeschwindigkeit. Es wurde also der Radhalbmesser als gegeben vorausgesetzt und daraus die Fahrgeschwindigkeit berechnet. Jetzt in der zweiten Formel bzw. Funktion ist es genau umgekehrt. Sie können sich vorstellen, dass die Umkehrung einer Funktion in der Technik nicht immer sinnvoll ist.
n(v)
Ob Sie nun 'n(v)' oder 'f(x)' schreiben, es ist eigentlich egal. Wichtig ist also nicht die Bezeichnung der Variable vor der Klammer, sondern die in der Klammer, denn das ist die unabhängig Veränderliche.
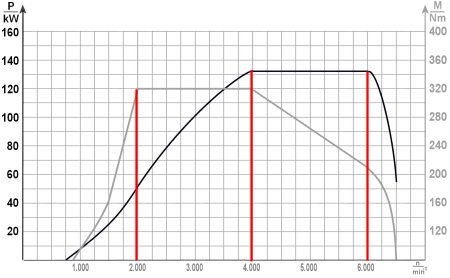
Im Kfz-Bereich ist es durchaus üblich, eine zweite Linie mit zugehöriger y-Achse rechts zu platzieren. Voraussetzung ist, dass sie die gleichen Werte der x-Achse benutzen. Überhaupt geht das nur mit zwei y- und nicht mit zwei x-Achsen. Grundsätzlich wird auf der x-Achse der Zahlenwert der unabhängigen und auf der y-Achse der Zahlenwert der abhängigen Variable abgetragen. Es wird also immer eine Drehzahl vorgegeben und dann die zugehörige Leistung bzw. das Drehmoment gesucht, nicht umgekehrt.
Deshalb auch die Bezeichnung 'f(x)' an der y-Achse. Dabei ist das 'f' weniger wichtig, man könnte auch 'g(x)' sagen. Wichtig ist hingegen, dass diese Werte in Abhängigkeit von 'x' entstehen bzw. entstanden sind, was durch die zusätzliche Klammer ausgedrückt wird. In diesem Fall hier ist also entweder die Leistung abhängig von Drehmoment und Drehzahl oder das Drehmoment abhängig von Leistung und Drehzahl dargestellt.
Oben im Diagramm ist also die Leistungskurve dunkel und die Drehmomentkurve hell eingezeichnet. Wichtig ist, beide Kurven sind miteinander verbunden über die Formel:
M · n
P =
9.550
Ändert sich das Drehmoment, so auch die Leistung und umgekehrt. Die Formel enthält eigentlich ein unnützes Element, nämlich die Zahl 9.550. Die macht nur Sinn für die Bequemlichkeit, die Werte nicht in ihren Dimensionen anpassen zu müssen. Man kann also das Drehmoment in Nm und die Drehzahl in min-1 einsetzen und erhält die Leistung in kW. Weiter unten wird erklärt, wie das zustande kommt. Rein mathematisch würde man also die Formel so schreiben:
P = M · n
Und jetzt sollten Sie sich einmal den Teil der jeweiligen Linie anschauen, der waagerecht verläuft, besonders, wie die andere Linie darauf reagiert. Waagerechter Verlauf bedeutet nämlich, dass sich der x-Wert nicht ändert, also M mit einer Konstanten multipliziert bzw. P durch eine Konstante dividiert wird. Das sind exakt die Verhältnisse, wie sie in Funktionen 1 durch f(x)=2x, f(x)=3x und f(x)=4x beschrieben werden.
Verläuft also die Drehmomentlinie waagerecht, steigt die Leistungslinie linear an (Multiplikation). Ist die Leistungslinie waagerecht, fällt die Drehmomentlinie linear ab (Division):
P
M =
n
Natürlich müssen beide Kurven nach der Formel ganz oben exakt zusammenpassen. Man bräuchte also nur die eine und könnte daraufhin die andere ausrechnen. Da aber meist sehr grob gezeichnet wird oder überhaupt kein Diagramm herausgegeben wird, kann man die Genauigkeit der Hersteller schlecht überprüfen. Allerdings ist es in diesem Fall möglich, weil der Hersteller folgende Angabe macht:
Drehmoment 320 Nm von 2000 - 3940/min
Leistung 132 kW von 3940 - 6000/min
Seltsam, diese Drehzahl von 3940/min, aber sie macht Sinn. Denn rechnet man P = M · n / 9550 mit P = 320 Nm · 3940 / 9550 dann ergibt das exakt die 132 kW an dieser Stelle. Umgekehrt ergibt das Drehmoment aus den Leistungswerten ebenso die 320 Nm. Weil also hier das maximale Drehmoment vom Drehzahlbereich her an die maximale Leistung stößt, können Sie (nur an dieser Stelle) die Konsistenz der Daten überprüfen.
Wie erklärt sich die Zahl 9550?
P = F · v Wir gehen von dieser Formel aus.
F · d · ? · n
P = ________________________________________
60
Die Geschwindigkeit v wird ersetzt durch die Drehzahl n mal dem Kreisumfang d · ?. Die Drehzahl wird pro Minute, die Geschwindigkeit pro Sekunde gemessen. Dadurch ergibt sich die Teilung durch 60.
M · 2 · ?· n
P = ________________________________________
60
Der Durchmesser d wird durch den doppelten Radius 2 · r ersetzt. Dann ergibt sich das Drehmoment M aus der Kraft mal dem Radius F · r.
M · n
P = ________________________________________
9550
Soll die Leistung in kW ausgegeben werden, kommt unter dem Bruchstrich der Faktor 1000 hinzu. 1000 · 60 / 2 · ? ergibt dann den Umrechnungsfaktor 9550, wenn man ? als 3,14 nimmt und entsprechend abrundet.
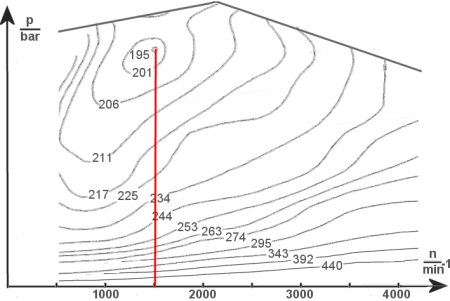
Bei 1500/min und ziemlich viel Druck im Brennraum hat dieser Motor seinen günstigsten spezifischen Verbrauch in g/kW·h. Das heißt nicht, dass hier auch der niedrigste Kraftstoffverbrauch ist, denn, wie Sie schon aus der Einheit sehen können, hängt der auch von der Leistung ab. Nehmen wir an, Sie möchten mit den verschiedenen hier angebotenen Werten und Leistungen rechnen, aber immer einen Verbrauch in Liter erhalten.
Es gibt also zwei Formeln:
be · Pe
B =
1000
B
=
?
Es müsste also zunächst 'B' und dann ' ' ausgerechnet werden. Verwirren lassen sollten Sie sich von dem Punkt nicht, er macht aus einem Volumen einen Volumenstrom, also ein Volumen pro Zeiteinheit. So wie Sie bei einem Volumen grundsätzlich eine Längeneinheit hoch 3 oder ein Maß in Liter erwarten, gehört beim Volumenstrom das pro Sekunde, Minute oder Stunde dazu.
Trotzdem wollen wir partout vermeiden, jedes Mal den Wert von der einen in die andere Formel einsetzen zu müssen.
be · Pe
1000
=
?
Zugegeben, das sieht zunächst wie ein Monster aus. Wer aber die Regel anwendet, dass man einen Bruch durch eine Variable dividiert, indem man sie mit seinem Nenner multipliziert, der kommt hier schnell zum Ziel:
be · Pe
=
1000 · ?
So, das war jetzt die Substitutions- oder Einsetzmethode. Dazu löst man die eine Formel nach einer bestimmten Variablen hin auf. Anschließend ersetzt man sie in der anderen Formel durch den restlichen Term. Es gibt noch die Möglichkeit, beide Formeln auf die gleiche Variable hin zu verändern:
be · Pe
B =
1000
B = · ?
Sind bei zwei Formeln die Terme auf der linken Seite gleich, so sind es auch die auf der rechten. Also kann man die durch ein Gleichheitszeichen miteinander verbinden. Die Division durch ? auf beiden Seiten führt wieder zum gleichen Ergebnis.
be · Pe
· ? =
1000
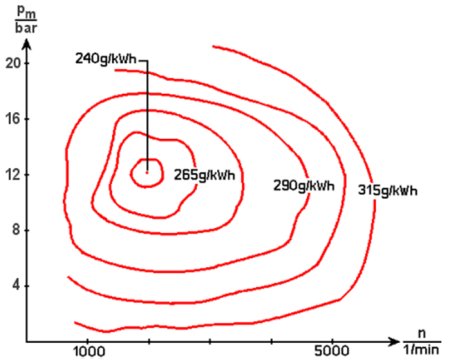
Hier noch einmal die beliebten Muschelkurven, die es wohl nur noch so lange gibt wie den Verbrennungsmotor. Dabei ist die Beschriftung der Achsen noch relativ leicht zu verstehen, unten die Drehzahl, davon abhängig der effektive Mitteldruck. In der Praxis sind die Kurven z.B. durch eine größere Anzahl noch komplexer. Wir haben sie für dieses Buch ein wenig vereinfacht.
Es wird immer dann komplizierter, wenn man zu zwei Variablen noch eine dritte braucht. Das ist hier der spezifische Kraftstoffverbrauch. Vielleicht wird es für Sie einfacher, wenn Sie sich die Fläche zwischen x- und y-Achse liegend vorstellen und die Kurven als Höhenlinien. Da allerdings die Werte zur Mitte hin fallen, entsteht kein Berg sondern eine nicht ganz konzentrische Senke.
Aus einem Diagramm mit Kennlinien ist jetzt ein Kennfeld geworden. Ein bekanntes Beispiel finden Sie nachfolgend von Bosch, bei dem der Zündwinkel abhängig von Drehzahl und Last bestimmt wird. Und wenn ein solches Kennfeld bzw. die dahinterstehenden Werte bestimmt ist, lässt es sich nahtlos in ein Steuergerät integrieren.
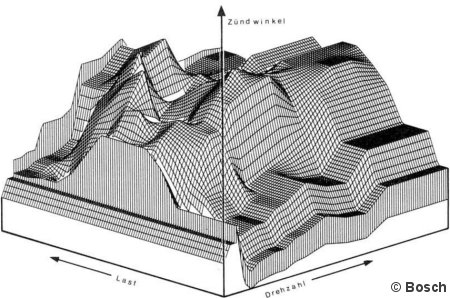
Es geht also im Diagramm ganz oben um die wichtige Aufgabe, den günstigsten Kraftstoffverbrauch zu erreichen. In erster Näherung könnte man anpeilen, möglichst den Motor immer im Bereich von 2000/min zu halten, aber wie bezieht man die Last ein.
Der mittlere effektive Druck pmeist der über alle Zylinder und deren jeweils vier Takte gemessene Druck pmi, abzüglich einen sogenannten Reibmitteldrucks, der die Verluste berücksichtigt. Er ist nicht nur vom Fahrerwunsch (Gaspedal) abhängig, sondern auch von dem z.B. an der Kupplung abgegriffenen Drehmoment.
Sie erreichen die 240 g/kWh also z.B. dann, wenn die Steigung der Strecke Sie zu etwa Halbgas zwingt, um die 2000/min zu halten. Geben Sie mehr Gas, steigen Last und Drehzahl und Sie fahren in dem Diagramm nach oben rechts. Aber das heißt noch lange nicht, dass Ihr Verbrauch jetzt gemächlich beim Erreichen der 265er Linie um 10 und der 295er noch einmal um 10 Prozent steigt. Denn das ist ja nur die Masse an Kraftstoff bezogen auf eine bestimmte Leistung. Und die ist natürlich auch gestiegen.
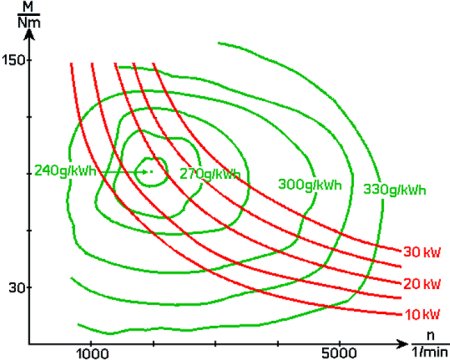
Das Motordrehmoment verhält sich wie der mittlere effektive Innendruck, sodass diese in etwa den gleichen Sachverhalt zeigt. Durch die zusätzlich eingezeichneten Leistungskurven wird hier deutlich, dass Sie u.U. zwar nur zwei Mal 10 Prozent spezifischen Kraftstoffverbrauch verloren haben, aber sich die erforderliche Leistung fast verdoppelt haben könnte. Hätten Sie also vorher sagen wir 5 Liter/100km verbraucht, so wären schon 20 und dann 80 % mehr schon 10,8 Liter/100km momentaner Verbrauch.
Also gehen sie ruhig in Richtung weniger Drehzahl und haben Sie keine Angst, das Gaspedal etwas stärker durchzutreten, solange Sie nicht schneller werden.
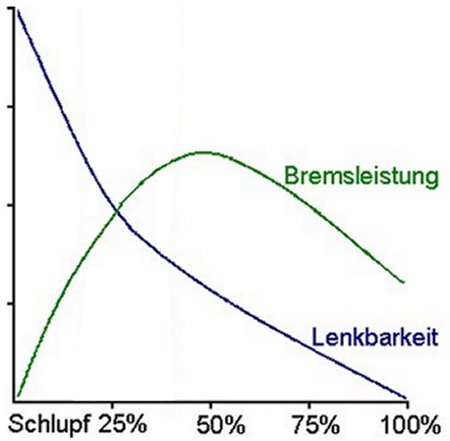
Keine Sorge, verglichen mit dem vorigen Kapitel wird es jetzt wieder etwas einfacher. Sie werden die beiden oben gezeigten Kurven in der entsprechenden Literatur mit etwas unterschiedlichem Verlauf finden. Aber den Sachverhalt, der hier angesprochen werden soll, betrifft das nicht. Denn auch hier behält die Mathematik ihre Exaktheit, wird aber überlagert von Ingenieurerfahrung.
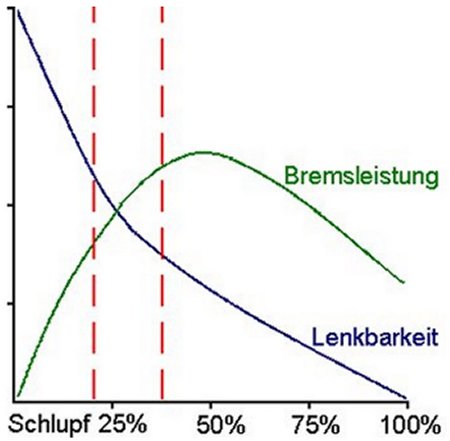
Es geht um die Frage, unter welchen Bedingungen ein ABS-System überhaupt ausgelöst werden soll. Dabei ist der auf der x-Achse eingetragene Schlupf der Anteil, um den das Rad schiebt statt zu rollen. Noch einfacher: Wenn das Rad auf einer Länge von 2 m, die dem Radumfang entspricht, nur eine halbe Umdrehung ausführt, hat es 50 Prozent Schlupf.
Schauen wir die Kurve der Bremsleistung an, so würde man deren Maximum exakt mit 50 Prozent Schlupf erreichen. Aber da ist noch die Lenkbarkeit, die wäre ungünstig gering. Also keine Chance, wenn denn diese wunderbare Bremsleistung nicht reicht, das Hindernis zu umfahren. Und hier setzt jetzt die Ingenieurleistung an. Fragen tauchen auf, die vielleicht nur in eingehenden Versuchen geklärt werden können.
Auf wie viel Bremsleistung kann/soll man verzichten und wie viel Lenkbarkeit gewährleistet noch eine entsprechende Reaktion des Fahrzeugs. Und wie groß ist der Abstand der beiden Regelgrenzen des ABS-Systems? Unten sehen Sie die Auflösung, die Werte, für die sich die Ingenieure abschließend entschieden haben. Deutlicher Verzicht auf Bremsleistung zugunsten von Lenkbarkeit.
bk Simmerath
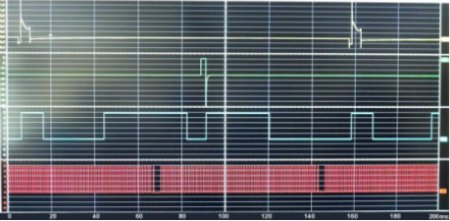
x-Achse in jeweils 20 Millisekunden aufgeteilt.
Hier sind wir dicht an der Praxis, obwohl dieses Bild auf einem Tester von einem Simulator erzeugt wurde. Aber so sehr weit weichen Simulatoren nicht von der Praxis ab, denn sie sind ja eine Zugabe zu den Geräten und dienen zum Üben.
Unten haben wir den Bezugsmarkengeber an der Kurbelwelle, darüber den Hallgeber an der Nockenwelle. Nach oben hin folgen die Signale für Saugrohr-Einspritzung und Zündung. Gezeigt werden uns mehr als zwei Umdrehungen, erkennbar u.a. an den beiden Zündsignalen ganz oben.
Sehr häufig wird exakt der Abstand zwischen zwei solchen Signalen angezeigt und auf der x-Achse mit 100 Prozent aufgelöst. Hier hingegen sind es Millisekunden, die uns schon eine erste Aufgabe ermöglichen, nämlich die Motordrehzahl zu berechnen. In der Vergrößerung ergeben sich für die erste Zündspannungsnadel etwa 6,5 ms weit von Null entfernt und die zweite 157,5 ms:
Bei 151 ms 2 Umdrehungen.
2
Bei 1 ms Umdrehungen.
151
2 · 60.000
Bei 60.000 ms Umdrehungen.
151
Die Motordrehzahl beträgt 795/min.
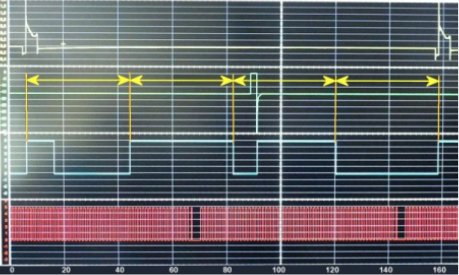
bk Simmerath
Jetzt sind wirklich nur noch etwas mehr als zwei komplette Umdrehungen sichtbar. Ganz unten der Sensor an der Kurbelwelle, der am Schwungrad ein Rad mit 58 kleineren und einer größeren Lücke abtastet. Die rechteckigen Signale pendeln zwischen 0 und 5 Volt. Das ist auch beim Nockenwellensensor darüber so, wobei man hier gut erkennen kann, dass es sich um einen Hallsensor handelt. Wichtig: Die vier Teile sind mit jeweils 180° alle gleich lang und zusätzlich invertiert.
Damit haben wir den Übergang von den Millisekunden zu den Winkeln. Oben schon berechnet entsprechen 720° bei der vorliegenden (Leerlauf-) Drehzahl ca. 150 ms. Erst die Winkel verraten uns, in welchem Takt wir uns befinden. Rechnet man den aus dem Diagramm entnommenen Abstand von ca. 83 ms durch Multiplikation mit 720 und Division durch 150 um, kommt man auf knapp 400°. Läge die Zündspannungsnadel genau auf OT, würde die Einspritzung 400° - 180° (Arbeitstakt) - 180° (Ausstoßtakt) = 40° im Einlasstakt beginnen.
Sie dauert übrigens 2,5 Millisekunden, was 12° entspricht. Bei ca. 1 Liter pro Stunde Leerlaufverbrauch, 800/min = 48.000/h, zwei Einspritzungen pro Umdrehung (Vierzylinder) und 2,5 ms pro Einspritzung würde 48.000 · 2 · 2,5 ms = 240.000 ms = 240 s lang eingespritzt. Bei 1,5 Liter = 1.500 ml Volumen geteilt durch die eben errechneten 240 s macht das 4,16 ml/s = 250 ml/min bzw. 0,25 Liter/min = 15 Liter/h. So viel schafft ein Einspritzventil, wenn man es mit Benzin unter dem hier vorherrschenden Druck versorgt und eine Stunde lang geöffnet hält.

Dieses wunderschöne Bild soll unser letztes Kapitel über Diagramme einleiten. Es zeigt ein Sechsganggetriebe einer Ducati Panigale 899 mit elektronisch steuerbarer Schaltwalze (Quick Shift) und Kettenrad zum Sekundärtrieb. Wir gehen von einem Motorrad aus, weil es da so richtig schön kompliziert wird. Wichtig, dazu eines mit Quermotor zu nehmen, denn beim Längsmotor sind wir schon fast wieder beim Pkw angelangt. Wer das Motorrad berechnen kann, hat dann mit dem Pkw keine Probleme mehr.
Ducati Panigale 899
Leistung 103 kW (140 PS) bei 10.750/min
Drehmoment 94 Nm bei 9.000/min
Primärantrieb Zahnradtrieb
Getriebe Sechsgang, automatisiert
Sekundärantrieb Kettenantrieb
Höchstgeschwindigkeit über 240 km/h
| Ducati Panigale 899 |
| Leistung | 103 kW (140 PS) bei 10.750/min |
| Drehmoment | 94 Nm bei 9.000/min |
| Primärantrieb | Zahnradtrieb |
| Getriebe | Sechsgang, automatisiert |
| Sekundärantrieb | Kettenantrieb |
| Höchstgeschwindigkeit | über 240 km/h |
Warum der Quermotor? Weil es hier neben dem Übersetzungsverhältnis des Getriebes selbst (iG) immer noch einen Primärantrieb vom Motor zum Getriebe (iP) und einen Sekundärantrieb vom Getriebe zum Hinterrad (iS) gibt. Der Primärantrieb ist eine Zahnrad- der Sekundärantrieb eine Kettenverbindung. Alle drei müssen multipliziert werden:
Aus der Bereifung hinten 180/60 ZR 17 lässt sich mit dem Faktor 25,4 für einen Millimeter bei 17 Zoll zunächst der Felgendurchmesser mit 431,8 mm ermitteln. Wenn das Verhältnis Höhe zur Breite 60 zu 100 oder 0,6 beträgt, muss dies mit der Reifenbreite von 180 mm multipliziert werden und man erhält 108 mm. Zusammen mit dem halben Felgendurchmesser ergibt sich ein rdyn von aufgerundet 270 mm.
Hier der nunmehr die Erweiterung des Datensatzes der Ducati Panigale 899:
Radhalbmesser rdyn = 0,27 m
Übersetzung (1. Gang) 37/15 = 2,467
Übersetzung (2. Gang) 30/16 = 1,875
Übersetzung (3. Gang) 27/18 = 1,5
Übersetzung (4. Gang) 25/20 = 1,25
Übersetzung (5. Gang) 24/22 = 1,09
Übersetzung (6. Gang) 23/24 = 0,96
Primär-Übersetzung 1,77
Sekundär-Übersetzung 44/15 = 2,93
| Radhalbmesser | rdyn = 0,27 m |
| Übersetzung (1. Gang) | 37/15 = 2,467 |
| Übersetzung (2. Gang) | 30/16 = 1,875 |
| Übersetzung (3. Gang) | 27/18 = 1,5 |
| Übersetzung (4. Gang) | 25/20 = 1,25 |
| Übersetzung (5. Gang) | 24/22 = 1,09 |
| Übersetzung (6. Gang) | 23/24 = 0,96 |
| Primär-Übersetzung | 1,77 |
| Sekundär-Übersetzung | 44/15 = 2,93 |
Getriebe iPrimär iGang iSekundär i Gesamt
1. Gang 1,77 2,467 2,93 12,79
2. Gang 1,77 1,875 2,93 9,72
3. Gang 1,77 1,5 2,93 7,78
4. Gang 1,77 1,25 2,93 6,48
5. Gang 1,77 1,09 2,93 5,65
6. Gang 1,77 0,96 2,93 4,98
| Getriebe | iPrimär | iGang | iSekundär | iGesamt |
| 1. Gang | 1,77 | 2,467 | 2,93 | 12,79 |
| 2. Gang | 1,77 | 1,875 | 2,93 | 9,72 |
| 3. Gang | 1,77 | 1,5 | 2,93 | 7,78 |
| 4. Gang | 1,77 | 1,25 | 2,93 | 6,48 |
| 5. Gang | 1,77 | 1,09 | 2,93 | 5,65 |
| 6. Gang | 1,77 | 0,96 | 2,93 | 4,98 |
Um die Werte in das Diagramm eintragen zu können, haben wir eine maximale Motordrehzahl von 11.500/min gewählt, denn der Motor leistet bei 900 cm3 unglaubliche 103 kW (140 PS) bei 10.750/min. Das folgende Diagramm zeigt auf der x-Achse n in 1/min und auf der y-Achse v in km/h.
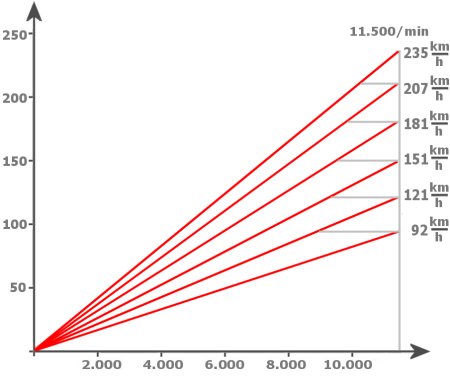
Wenn Sie die Geschwindigkeiten nachrechnen, tippen Sie bitte nicht für jeden Gang alle Zahlen ein. Berechnen Sie besser mit allen Variablen außer iG einen Wert von in diesem Fall 226, rechnen noch einmal nach und teilen ihn nacheinander durch die einzelnen Getriebe-Übersetzungsverhältnisse. Zu viel Tippen erhöht die Gefahr von Fehlern. Übrigens hilft bei der Überprüfung oft eine andere Reihenfolge, z.B. bei Summen oder Produkten.
Auf den ersten Blick ist zu erkennen, dass die von Ducati angegebene Höchstgeschwindigkeit von über 240 km/h noch nicht einmal bei 750/min über der Nenndrehzahl im höchsten Gang zu erreichen ist, also zu optimistisch angegeben ist. Unser rdyn ist zwar der ungenauste Kandidat in unserer Rechnung, wird auch mit der Geschwindigkeit durch zentrifugales Aufpumpen größer, aber vermutlich auch bei 235 km/h nicht erreicht.
Dann erkennt man sehr schön an den waagerechten Linien, bei welcher Drehzahl man landet, wenn man in jedem Gang den Motor voll ausdreht. Diese Drehzahl wird auch bei Getrieben im Pkw mit größerem Gang in der Regel immer höher, die waagerechte Linie also von unten nach oben immer kürzer. Allerdings würde man ein Pkw-Getriebe niemals so auslegen, dass der erste Gang bis über 90 km/h reicht. Dann wäre ja fast eine Beschleunigung auf 100 km/h ohne zu schalten möglich. Der erste Gang kann beim Motorrad nur deshalb so hoch ausgelegt werden, weil es so einen großes Drehzahlband und eine so kleine Masse hat.
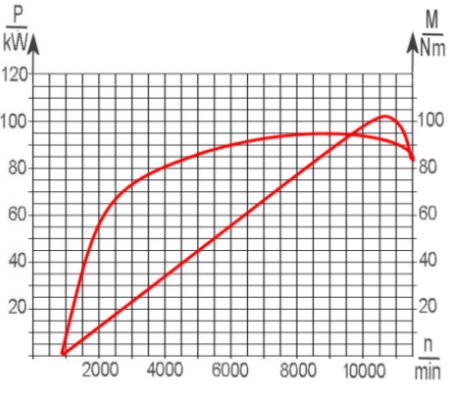
Wir haben jetzt die beiden Kurven nicht ausdrücklich unterschieden. Sie müssten eigentlich die buckelige, relativ früh ansteigende als die Drehmomentkurve der rechten Achse zuordnen können und die andere als Leistungskurve erkennen. Und wenn hier kurz vor 11.500/min geschaltet würde, wären mindestens 9000/min im nächst höheren Gang ideal. Und das ist bei dieser engen Gangabstufung laut Diagramm oben auch möglich. Im Gegenteil, man sollte mit höherer Geschwindigkeit die Grenzdrehzahl immer weniger ausnutzen.
Und wie sind die Kurven zustande gekommen? Zunächst war da die Leistungsangabe von 103 kW bei 10.750/min und die des Drehmoments von 94 Nm bei 9.000/min. Letzter ergab bei dieser Drehzahl 89 kW (siehe Diagramme 3). Aus der sich ergebenden Geraden konnten dann weitere Punkte für die Drehmomentkurve ermittelt werden. Sie sehen wie nah diese dem Maximum sind, also ist eine größere Krümmung der Leistungskurve ausgeschlossen. Eine gewisse Glättung der Wirklichkeit stellt so eine Kurve ohnehin dar.
MMotor nMotor MHinterrad vHinterrad
57 Nm 2000/min 700 Nm 15,9 km/h
81 Nm 4000/min 995 Nm 31,8 km/h
86 Nm 5000/min 1057 Nm 39,8 km/h
94 Nm 9000/min 1155 Nm 71,6 km/h
91,5 Nm 10750/min 1124 Nm 85,5 km/h
| MMotor | Drehzahl | MHinterrad | Geschwindigkeit |
| 57 Nm | 2.000/min | 700 Nm | 15,9 km/h |
| 81 Nm | 4.000/min | 995 Nm | 31,8 km/h |
| 86 Nm | 5.000/min | 1.057 Nm | 39,8 km/h |
| 94 Nm | 9.000/min | 1.155 Nm | 71,6 km/h |
| 91,5 Nm | 10.750/min | 1.124 Nm | 85,5 km/h |
Im nächsten Diagramm sollen die Drehmomente am Hinterrad auf die Fahrgeschwindigkeit bezogen werden. Ersteres erhält man relativ einfach, indem man die Motordrehmomente bei den einzelnen Drehzahlen mit der Gesamtübersetzung multipliziert. Oben in der Tabelle ist das für den ersten Gang beispielhaft aufgelistet. Da werden dann aus 57 Nm am Motor 700 Nm am Hinterrad. Und das geht dann für die anderen Drehmomente so weiter.
Die Drehzahlen kann man beliebig auswählen, je nachdem, wieviel Stützstellen man braucht, um eine einigermaßen genaue Kurve zeichnen zu können. In einem zweiten Schritt wird dann mit Hilfe der Formel ganz oben die Fahrgeschwindigkeit bei den einzelnen Motordrehzahlen berechnet und diesen zugeordnet. Wie gesagt, die Tabelle oben zeigt nur diese Berechnung für den ersten Gang, an den anderen können Sie sich selbst einmal versuchen, Ergebnisse im folgenden Diagramm.
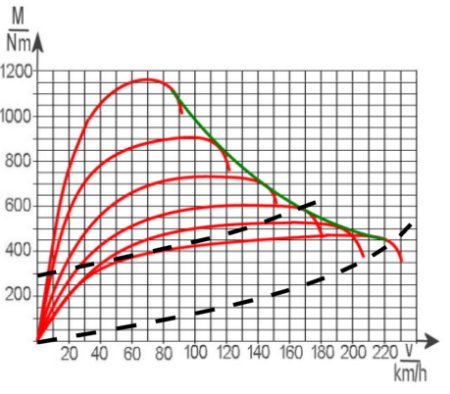
Das Endergebnis unserer Untersuchung. Hier sehen Sie die Zugkraft oder besser das Zugdrehmoment der Ducati in den einzelnen Gängen bezogen auf die Fahrgeschwindigkeit. Das Drehmoment hinten nimmt mit länger werdender Übersetzung immer mehr ab, neben den größer werdenden Verlusten z.B. durch Luftwiderstand mit ein Grund, warum die Beschleunigung mit zunehmender Geschwindigkeit immer mehr abnimmt.
Interessant ist die zusätzlich eingezeichnete Kurve. Sie wurde so eingesetzt, dass sie Berührung mit jeder der sechs Drehmomentkurven hat. Im Idealfall ist es eine Hyperbel. Wenn Sie sich deren beiden Enden bis ins Unendliche verlängert denken, dann nähern die sich immer mehr den beiden Achsen an. Zweite Bedingung für eine Hyperbel, sie soll klappsymmetrisch zur x/y-Diagonale sein, also sich auf beiden Seiten mit gleichem Abstand nähern.
Was aber bedeutet diese zusätzliche Kurve kfz-technisch? Sie stellt sozusagen eine Ideallinie dar. Sie vermeidet die Verluste, die durch die Stufung der Gänge der Zugkraft an Verlusten zugefügt werden, wobei eventuelle Schaltpausen hier unberücksichtigt sind. Hätten wir also, bei Motorrad ungewöhnlich, eine variable Übersetzung z.B. durch Ketten-Umschlingung, so könnte diese Kurve dabei herauskommen.
Weil aber besonders in Europa sich die Autofahrer(innen) nicht daran gewöhnen konnten, dass sich die Übersetzung zur Hinterachse trotz annähernd gleicher Motordrehzahl änderte, mussten die Hersteller künstliche Stufungen einprogrammieren, was natürlich einen Rückfall in die oben abgebildeten Einzelkurven bedeutete. Der europäische Mensch erwartet, dass bis zum nächsten Schalten die Motordrehzahl synchron zur Fahrgeschwindigkeit steigt. Z.B. sind solche Getriebe in Asien nach wie vor beliebt.
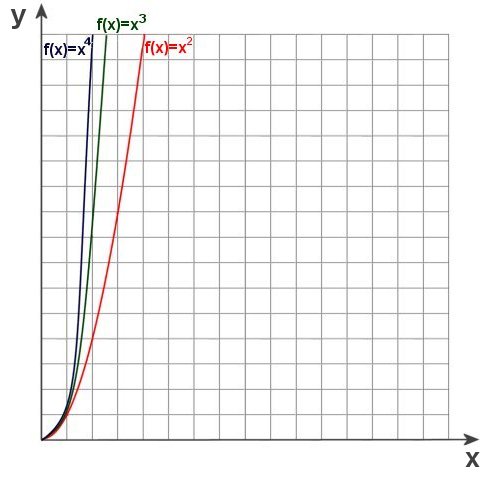
Die senkrechte Achse wird y-Achse oder auch Ordinate genannt, die waagerechte x-Achse oder Abzisse. Beachten Sie, wie sich die Potenzen auf die zeichnerische Darstellung auswirken. Sie können das durch das Raster leicht nachvollziehen, indem Sie rechnen:
Sie sehen, der Graph der Funktion steigt rascher, je größer der Exponent wird. Aber alle Graphen müssen durch y=0/x=0 und f(x)=1/x=1. Das ist übrigens bei den nächsten Graphen auch so, die durch Multiplikation entstehen.
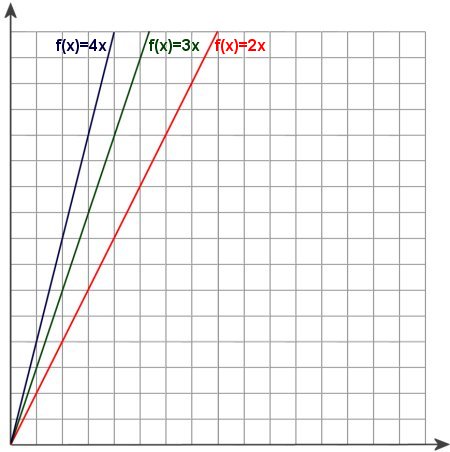
Funktionen, die ausschließlich Punkt- bzw. Strichrechnung mit einer Zahl (Konstanten) beinhalten, werden als Geraden abgebildet. Man spricht auch von 'linearen' Funktionen. Erstere bestimmen dabei die Steigung, letztere die Verschiebung auf der y-Achse.
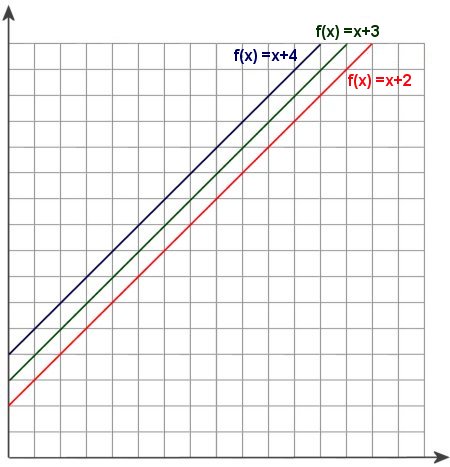
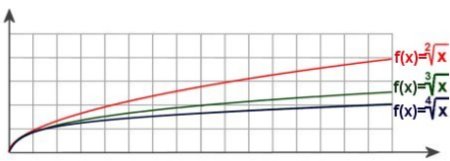
Zum Schluss die zum obersten Diagramm passenden zweiten, dritten und vierten Wurzeln. Man erkennt sofort die Spiegelung der Graphen bei ansonsten gleichem Verlauf.
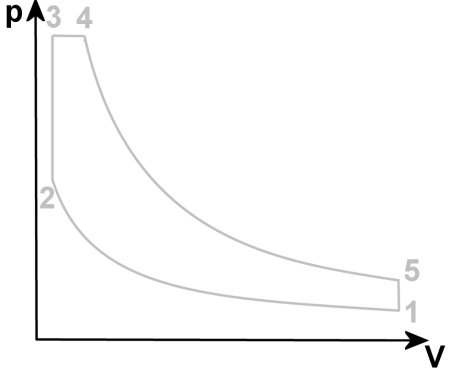
Im Kapitel Diagramme 3 wurde schon auf den Unterschied zwischen einer Funktion und Messergebnissen hingewiesen, die beide zu einem 'Funktionsgraphen' führen, also einer bildlichen Darstellung. Sehen wir uns dazu im Bild oben den sogenannten Seilinger-Prozess von einem Hubkolben an:
1 -> 2 Isentrope Verdichtung (ohne Wärmezu-/abfuhr)
2 -> 3 Isochore Verbrennung (ohne Raumänderung)
3 -> 4 Isobare Verbrennung (ohne Druckänderung)
4 -> 5 Isentrope Entspannung (ohne Wärmezu-/abfuhr)
5 -> 1 Isochorer Ladungsausstoß (ohne Raumänderung)
Es handelt sich also um theoretische Kurven, alle mit ausgewiesenen Funktionsvorschriften. Die gestatten es den Ingenieuren/innen, schon einmal, z.B. den zu erwartenden maximalen Wirkungsgrad auszurechnen.
Warum ist das Diagramm oben so weit weg von dem realen Prozess? Weil z.B. der komplette Ladungswechsel nicht berücksichtigt wurde. Auch die Reibung der Lager und des Kolbens sind nicht berücksichtigt, Pumpverluste ebenfalls nicht. Auch kann und soll die Wärme weder beim Verdichten noch im Arbeitstakt komplett im Zylinderraum gehalten werden.
Am besten lässt sich der Nachteil eines theoretischen Konstrukts am Beispiel der oberen waagerechten Linie von 3 nach 4 erklären. Hier wird angenommen, dass der Wärmeeintrag durch die Verbrennung exakt gleich dem Verlust durch den geringer werdenden Druck beim Weg des Kolbens nach UT sei. Und das womöglich auch noch für jeden Betriebszustand.
An Oldtimern ist nach Einbau von Ventilsitzringen (Umstellung auf bleifreies Benzin) eine Erhöhung der Verdichtung für den Betrieb mit Superbenzin möglich. Es soll eine Formel entwickelt werden, aus der durch Eingabe von Hub, altem und neuem Verdichtungsverhältnis die Höhe der Materialabtragung direkt hervorgeht. Grundlage ist die in Gleichungen 3 erarbeitete Formel:
Vh
Vc =
? - 1
Zu dieser brauchen wir jetzt noch eine weitere Formel:
Vc' = Vc1 - Vc2
Da der unteren Teil eines Verdichtungsraums Teil des Zylinderraums ist, können wir hier die Formel für den Zylinder Vh = A · h anwenden:
A · s' = Vc1 - Vc2 | : A
Vc1 - Vc2
s' =
A
Jetzt setzen wir die Formel ganz oben zwei Mal in diese hier ein, so wie wir das im vorigen Kapitel gelernt haben. Allerdings als kleine Variante einmal mit dem Index 1 für den Verdichtungsraum vor der Materialabtragung und dem Index 2 danach:
Man darf bei einer Summe, hier '?1 - 1' und '?2 - 1', jeden Summanden einzeln nicht nur mit der gleichen Zahl/Variablen multiplizieren sondern natürlich durch die gleiche Zahl/Variable ' A' teilen. Im weiteren Verlauf wenden wir noch einmal die Formel für den Zylinder 'Vh= A · s' an und zwar in der Umkehrung 's = Vh/A'. Damit können wir 'Vh /A' in beiden Brüchen durch 's' ersetzen:
s s
Vc = -
?1 - 1 ?2 - 1
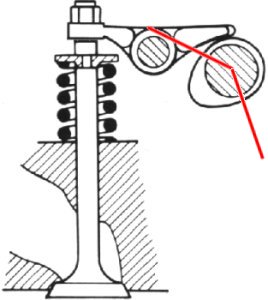
Textaufgaben bergen die Schwierigkeit, einen geschilderten Sachverhalt konkret und möglichst vollständig zu erfassen und dann in eine mathematische Schreibweise umsetzen zu müssen. Hilfe könnte ein Schema bieten. Hier eine einfache Beispielaufgabe zur Anwendung dieses Schemas:
Wenn ein Einlassventil 35° vor OT öffnet und 56° nach OT schließt, wie groß ist dann bei 6000/min der Kurbelwelle die Ventilöffnungszeit?
Geg.: ? = 35° + 180° + 56° = 271°,
n = 6000/min
Ges.: t in s
?
Formel: t =
6 · n
271°
Rechnung: t =
6°·min/s · 6000/min
Ergebnis: t = 0,0075 s = 7,5 ms
Sollten Sie sich fragen, warum die Konstante '6' im Nenner mit so einer seltsamen Einheit '°·min/s' versehen ist, so geschieht das der Ordnung halber. Es ist einfach so, dass auch Einheiten so weggekürzt werden müssen, damit am Schluss die 's' übrigbleibt.

Wer Gold sucht, muss sich entweder mit kleinen Funden zufrieden geben, oder in viel Technik investieren, immer vorausgesetzt, der Boden gibt das auch her. Wir gehen jetzt von 240 Kubikmeter pro Stunde aus, mit der eine Waschanlage gefüttert werden muss.
Leider steht sie 1 Kilometer entfernt von der Schürfstelle. Es sind 4 Lkw (Bild) nötig, wenn jeder 2 Minuten zum Laden braucht, 3 Minuten lang fährt und in einer Minute ablädt. Wie viele Lkw spart man ein, wenn man die Waschanlage in höchstens 100 Meter Entfernung aufstellt? Taktzeit dann 3,3 Minuten.
4 Lkw 6 Minuten Taktzeit 240 m3
240
1 Lkw 6 Minuten Taktzeit m3
4
240 · 6
1 Lkw 1 Minute Taktzeit m3
4
240 · 6 · 2
2 Lkw 1 Minute Taktzeit m3
4
240 · 6 · 2
2 Lkw 3,3 Minuten Taktzeit m3
4 · 3,3
Hier haben Sie die klassische Struktur eines sogenannten 'verallgemeinernden' Dreisatzes. Sie können natürlich schon im zweiten Schritt für beide unabhängig Veränderliche auf die Einheit schließen und in einemdritten und letzten Schritt beide auf die erforderlichen Größen setzen. Wir raten aber zu fünf Sätzen, weil z.B. in diesem Fall zunächst dividiert und dann multipliziert werden muss. Theoretisch können Sie jetzt auch noch mehr unabhängig veränderliche Variable einbinden.
Zugegeben, man hätte es sich denken, können, dass bei fast halbierter Fahrzeit sich die Anzahl der benötigten Lkw ebenfalls halbiert. Immerhin weiß man jetzt, dass die beiden verbleibenden Lkw ihre Transportleistung um ca. 10 Prozent steigern müssen. Heraus kommen 218 m3
Ganz wichtig ist hier, die Werte ohne Berechnung zusammen zu fassen und erst am Ende den Taschenrechner zu benutzen, weil dieser dann nur einmal rundet. Auch ist beim Eintippen zu beachten:
240 mal 6 mal 3 geteilt durch 4 geteilt durch 3,3
Man kommt leicht in Versuchung, statt durch 3,3 zu teilen, mit 3,3 malzunehmen.

Der Land Rover Discovery soll 'bis zu' 480 kg leichter geworden sein.
Bestimmt haben Sie bei den entsprechenden Kapiteln geahnt, dass die Bruch- und Prozentrechnung mit einander verwandt sind. Man kann also Brüche in Prozent ausdrücken und umgekehrt. So sagt man lieber, man möchte ein Drittel haben statt 33,33 Prozent. Umgekehrt käme aber wohl kaum jemand auf die Idee, eine Majorität von 51 Prozent als Bruch ausdrücken zu wollen.
Glücklich der- oder diejenige, der/die zwischen beiden Rechenarten problemlos hin- und herschalten kann. Natürlich ist die Frage nach 20 Prozent von 20 Prozent selten. Aber was antworten Sie da, vielleicht 40 Prozent? Hoffentlich nicht. Bedienen Sie sich der Bruchrechnung, bei der 20 Prozent ein Fünftel ist. Und mit einem Fünftel von 20 Prozent bewegen Sie sich sehr in die richtige Richtung.
Seien Sie vorsichtig mit Begriffen wie der 'einzigste' und Zahlen über 100 Prozent. Da wird der Zähler langsam größer als der Nenner. Man nennt solche Brüche nicht umsonst auch 'unecht'. Es sind erste Schritte zu luftigen Versprechungen, denen man mit ein wenig Nachdenken ansieht, dass niemand vorhat, sie einzuhalten.
Was nutzt es, wenn ein Laden 'bis zu' 20 Prozent Rabatt verspricht. Da kann auch die Bruchrechnung nicht helfen, wenn 'bis zu' ein Fünftel Preisnachlass geboten würde. Der neue Land Rover wird 'bis zu' 480 kg leichter. Wer weiß, mit welcher utopischen Zusatzausstattung, die Sie sich ohnehin nicht leisten wollen oder können.
Zwingen Sie sich, den durchgestrichenen Preis bewusst zu überdenken, wenn Sie es schon nicht geschafft haben, ihn zu übersehen. Lassen Sie sich keineswegs von Preisen treiben, die nur noch bis 16 Uhr ihre Gültigkeit haben. Überlegen Sie nicht nur, was Sie mit dem angebotenen Teil wirklich anfangen können, sondern auch, welches Sie, zuhause angekommen, dafür dann eigentlich entsorgen müssten.
Wissen Sie, wozu z.B. der Fernseher eine Fernbedienung hat? Weil Sie damit in den Werbepausen den Ton abschalten können. Denn anders haben Sie gegen die Sprüche keine Chance. Spätestens, wenn Sie sich dabei erwischen, so etwas am nächsten Tag nach zu trällern, ist unbedingtes Handeln geboten. Glauben Sie mir, je dämlicher der Spruch, desto schwerer ist er zu entsorgen.
Allerdings ist keine Regel ohne Ausnahme anzuwenden. Da verbringen Sie einen wunderschönen Urlaub im sonnigen Süden. Sie wissen genau, Sie werden gerade über den Tisch gezogen, aber der Ring sieht an ihrer Hand wirklich bezaubernd aus. Und wie wollen Sie demnächst so eine Situation noch einmal herstellen? Schon lange hatten Sie so ein Geschenk vor. Und fragen Sie in aller Zukunft niemals nach, was der Ring angeblich wirklich wert ist!

Diesmal haben Sie vielleicht wirklich Schwierigkeiten, den Zusammenhang zwischen dem Bild oben und einer Einführung in die Geometrie zu erahnen. Dargestellt sind Leder und einige wenige Werkzeuge, es zu verarbeiten. Das wäre dann teure Handarbeit. Wenn Sie aber an eine größere Serienproduktion mit sehr vielen und vielfältigen Stücken denken, da muss der Computer helfen.
Das sorgfältig bearbeitete, ziemlich viel größere Tierfell kommt in die Produktion. Unvermeidlich, dass es noch Fehler aufweist, z.B. Narben, wo das Tier in den Zaun geraten ist. Diese müssen sorgfältig mit einem Spezialstift umkreist werden, wobei es sogar von beiden Seiten angeschaut wird. Und man fragt sich, wann die denn mit dem Ausschneiden beginnen.

Gar nicht, denn danach wird das Fell auf den Arbeitstisch einer Kombination aus Scanner und Schneidemaschine gelegt. Und die berechnet jetzt um die auszusparenden Stellen alle Teile, die sie von dem auszustattenden Modell gespeichert hat. Da bleibt dann so wenig ausgenutzter Raum übrig wie möglich. Im zweiten Teil werden diese Teile dann relativ rasch ausgeschnitten.
Unten sehen Sie, aus wie vielen Teilen schon ein Kindersitz bestehen kann. Nach dem Ausschneiden der Stücke müssen diese natürlich noch mit Ziernähten verbunden und gepolstert werden. Aber ein wesentlicher Teil der Arbeit ist dann doch schon vom Computer übernommen worden.

Um uns langsam der Geometrie weiter nähern zu können, geht es hier zunächst nur um Längen. Also sind eigentlich nur mm, cm, dm oder m zu addieren. Das ist bei graden Stücken kein Problem, aber es sind auch Bögen dabei. Von diesem Moment an kann man die Länge nicht mehr nur außen bestimmen.
Es geht um eine Art 'neutrale Faser', wie wir sie vom Biegen her kennen. Eine Art Mittellinie, die dort weder gestreckt noch gestaucht wird. Wenn das da oben eine Landstraße wäre, müssten wir sie als Mittellinie einzeichnen. Deren Länge gilt es zu berechnen.
Dazu braucht man, wie auch bei der Berechnung eines Vollkreises, die sogenannte Kreiszahl ?. Obwohl sie eine Konstante ist, gehört sie nicht dem gewohnten Zahlensystem an, sondern ist eine sogenannte irrationale Zahl, also nicht exakt bestimmbar, so viele Nachkommastellen man von ihr auch betrachten möge.
Trotzdem ist das Verhältnis von Umfang zum Radius bei jedem Kreis gleich, ebenso wie das eines Kreises zu einem in umgebenden Quadrat. Wir rechnen mit ? als 3,14 oder drücken die entsprechende Taste auf dem Taschenrechner. Wenn wir also oben die Mitte zwischen dem jeweils kleinen und dem großen Viertelkreis gefunden haben, brauchen wir die nur noch mit ? zu multiplizieren.
Davon zwei Mal ein Viertel bzw. einmal die Hälfte nehmen und die Länge durch die S-Kurve steht fest. Rechts käme nur noch ein Achtel eines entsprechenden Kreisbogens hinzu. Stellen die Kurven keine einfache Teilung eines ganzen Kreises dar, muss man halt den jeweiligen Winkel auf 360° beziehen.
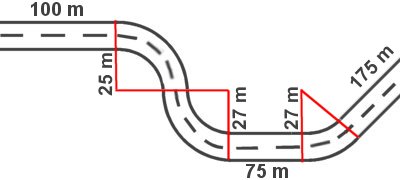
Leicht lassen sich die graden Stücke zu 350 m addieren. Nehmen wir jetzt an, die Straße sei 10 m breit, dann müssen von den Radien jeweils 5 m abgezogen werden. Sehr wichtig ist, dass Sie diese verdoppeln, wenn Durchmesser in die Formel eingesetzt werden müssen. Hier die Formel, nach der gerechnet werden kann:
d · ? · ?
b =
360°
40 m · ? · 90°
b1 =
360°
44 m · ? · 135°
b2 =
360°
Aus dem verdoppeltem Radius von (25 - 5) · 2 m = 40 m ergibt sich b1 mit 31,4 m. Der Radius der beiden Kurven weiter links beträgt (27 - 5) · 2 m = 44 m. Bei gleichem Radius kann man ihre Winkle mit 90° und 45° zusammenfassen. So beträgt dann b2 51,8 m, was eine Gesamtlänge der Straße von 433,2 m ergibt.
Frage im Fernseh-Quiz: Warum sind Kanaldeckel rund und nicht eckig, z.B. quadratisch?
Antwort: Weil runde Deckel nicht in das Loch fallen können, das sie abdecken. Der quadratische würde hineinpassen, weil seine Diagonale deutlich größer ist als eine Seite.
Wir setzen die Formeln zur Berechnung der einzelnen Flächeninhalte voraus. Spannend wird es erst, wenn wir in den Baumarkt geben, um Bodenplatten zu kaufen. Nehmen wir einmal Platten der Größe 20 cm x 20 cm bei einer Fugenbreite von 1 mm. Wie viele Platten passen in einen Raum mit 24 m2 Größe. Und kommen Sie mir ja nicht mit dem Argument, man kauft immer ein paar mehr als Reserve. Auch dazu sollte man erst einmal die Grundmenge bestimmen.
Und es scheint doch so einfach, denn 0,21 m · 0,21 m ergibt 0,0441 m2. 24 m2 geteilt durch 0,0441 m2 hat 544,2 Platten als Ergebnis, also 545. Das ging doch schnell oder? Ist es eigentlich egal, ob die Raummaße 6 m * 4 m betragen oder 5,1 m x 4,7 m. Sie ahnen schon, es ist nicht egal.
Geteilt durch 0,21 m . . .
4 m 19,05 Platten
4,7 m 22,38 Platten
5,1 m 24,29 Platten
6 m 28,57 Platten
Jetzt wird aufgerundet und multipliziert, 20 * 29 = 580 und 23 * 25 = 575. Schon daran erkennen Sie, dass für eine genaue Berechnung im Baumarkt die Fläche des Raumes nicht genügt. Und vielleicht vergleichen Sie einmal mit oben. Wir liegen 30 bis 35 Platten drüber.
Übrigens, bei 19,05 Platten könnte man auf die Idee kommen, dass 19 Platten reichen, weil ja noch eine Fuge hinzugerechnet werden müsste, aber das ist genauso spitzfindig, wie die Wiederverwendung der abgeschnittenen Plattenteile. 545 Platten reichen auch dann definitiv nicht

In den vorigen Kapiteln haben wir den Unterschied zwischen einer Funktion mit Funktionsvorschrift und einer grafischen Darstellung von Messwerten erklärt. Letztere werden z.B. mit so einem oben gezeigten Gerät ermittelt, um im Falle von zu schnellem Fahren Bußgeld eintreiben zu können.
Angefangen hat das mit der Aufnahme der Zeit beim Durchfahren einer gewissen Strecke. War die Zeit unterhalb eines Limits, dann war auch hier Bußgeld fällig. Im letzten Fall wurde eine Durchschnittsgeschwindigkeit über eine gewisse Strecke ermittelt, bei der Anlage oben im Prinzip die Geschwindigkeit an einem gewissen Punkt, der bisweilen bei solcher Art Messgeräten sogar auf der Fahrbahn eingezeichnet ist.
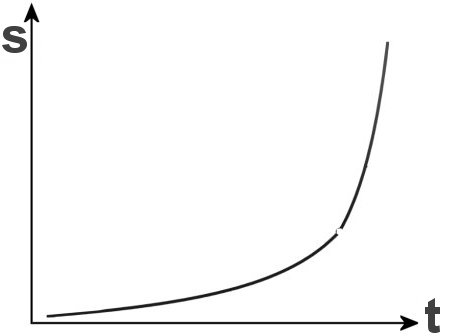
Und genau dazu wird die sogenannte 'Ableitung' verwendet. Es wäre die Steigung einer Tangente an dem eingezeichneten Punkt. Sie haben so eine Gerade schon kennengelernt:
f(x) = 2x f(x) = 3x f(x) = 4x
Dort wurde Ihnen erklärt, dass der Multiplikator von x die Steigung einer Geraden ergibt. Bei f(x) = 2x steigt das f(x) langsamer als bei f(x) = 4x. Und da die Steigung im Diagramm oben (s1 - s0) : (t1 - t0) oder ?s : ?t ist, entspricht sie exakt der Geschwindigkeit:
?s
v =
?t
Hier noch einmal das Diagramm. Von dem Punkt aus, bei dem wir die Geschwindigkeit bzw. Steigung bestimmen wollen, gehen wir um ?t weiter und erhalten eine um ?s verlängerte Strecke, die zurückgelegt wurde. Die Durchschnittsgeschwindigkeit auf dieser Strecke wird durch die Gerade 1 dargestellt.
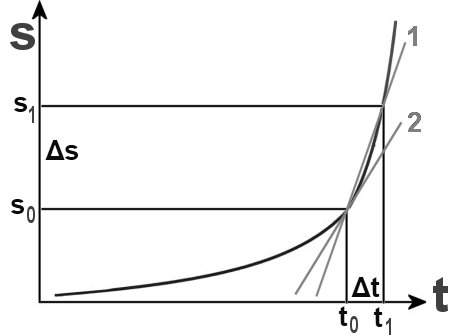
Das griechische ? (Delta) vor einer Variablen drückt einen Unterschied oder eine Differenz aus.
Bei der Bildung einer Ableitung kommt es darauf an, t1 jetzt langsam auf t0 zurückzuführen, also ?t Null werden zu lassen. Dadurch wird die Gerade 1 langsam zur Geraden 2, was dann eine Tangente an die Kurve exakt im Punkt t0 wäre. Wir schreiben das so:
Wenn man also einen unendlich kleinen Bereich an dem Punkt S0 und t0 der obigen Funktion betrachtet, kann man den Anstieg als linear annehmen und von diesem linearen Anteil hat die Differentialrechnung ihren Namen. Man geht hier aus von einer Differenz, oben z.B. von t1 - t0, die man immer kleiner werden lässt.
Wir sind also jetzt von der durchschnittlichen zur momentanen Geschwindigkeit gekommen. Geometrisch hat sich die Sekante, also eine Verbindung zweiter Punkte eines Kreisbogens, in eine Tangente gewandelt, mit also nur noch einem Berührpunkt, exakt dem, für den wir unsere Geschwindigkeit ermitteln wollen.

Wenn Sie dieses Bild mit dem vorigen vergleichen, könnten Sie meinen, es sei das gleiche nur mit einer anderen Beschriftung. Stimmt. Und doch soll es hier ausdrücken, dass es sich um eine Funktion handelt. Eine Kurve, die aus Messwerten gebildet wird, besteht eigentlich nur aus ein paar Stützstellen, die durch eine Linie verbunden werden.
Eine Funktion hingegen ist in jedem Punkt der Kurve exakt definiert. Und nur hier kann ich natürlich langsam vom Punkt f(x +?x) / x +?x auf f(x) / x zubewegen:
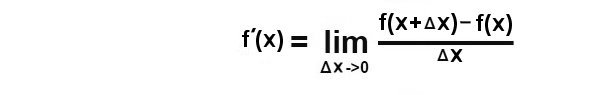
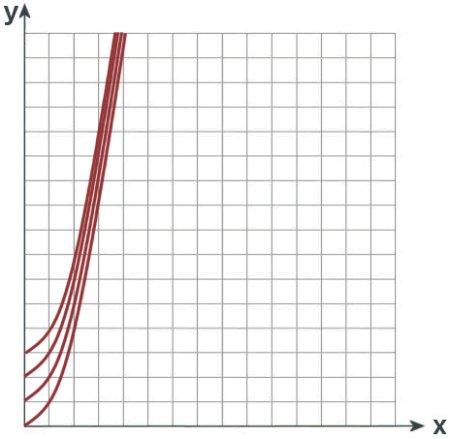
Um die Tangente an dem Graphen einer Funktion suchen zu können, muss dieser Graph natürlich eine Kurve sein. Die einfachste Funktionsvorschrift, die eine Kurve zum Graphen hatte war im Kapitel Funktionen 1
f(x) = x2
Außer f(x) = x2, die von Null ausgeht, haben wir im Diagramm oben noch drei Mal eine Konstante hinzugefügt, so dass die jeweils nächsthöhere Kurve entsteht:
f(x) = x2 + 1
f(x) = x2 + 2
f(x) = x2 + 3
Egal, welche der drei wir für unsere erste Berechnung der Steigung einer Tangente z.B. im Punkt 1/1, 1/2, 1/3 oder 1/4 auswählen, die Konstante hat keinen Einfluss darauf. Das beweist dann auch die Berechnung der ersten Ableitung einer dieser Funktionen:
f(x) = x2 + 1
f'(x) = (x + ?x)2 + 1 - (x2 + 1)
= x2 + 2 ?x · x + 1 -x2 - 1
2?x · x + ?x2
=
?x
= 2x +?x
Und da ja ?x Null werden soll, ist die erste Ableitung von f(x) = x2 + 1:
f'(x) = 2x
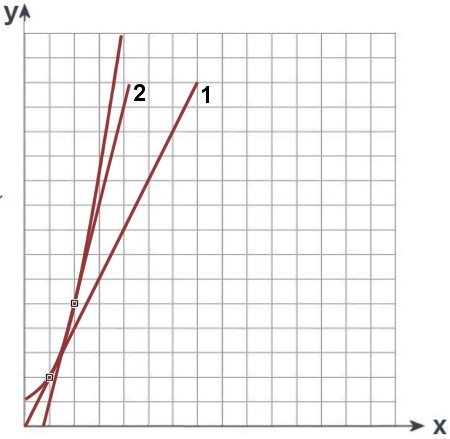
Setzen wir für x 1 ein, berührt die Grade 1 mit der Steigung 2 den Graph der Funktion im Punkt 2/1, setzen wir für x 2 ein, berührt die Grade 2 mit der Steigung 4 im Punkt 1/5.
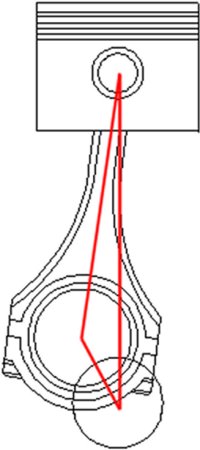
Hoffentlich auch für Sie eine durchaus praxisnahe Aufgabe: Ein Kurbeltrieb mit der Pleuelstangenlänge l steht in einem bestimmten Winkel ? zu OT. Welchen Weg muss er noch bis OT zurücklegen. Anders gefragt, wie ist die Umrechnung von Grad vor OT zu Millimeter vor OT?

Das gedrehte Dreieck aus dem halben Hub, Pleuellänge und der im Prinzip gesuchten Länge unten haben wir in zwei rechtwinklige Dreiecke aufgeteilt. Um die linke Teillänge unten zu bestimmen, brauchen wir die Formel:
x
sin ? =
s/2
Entscheidend ist der rechte Winkel, den wir durch die Aufteilung in zwei Dreiecke jeweils gewonnen haben. Der Sinus funktioniert nur bei rechtwinkligen Dreiecken. In denen ergibt sich gegenüber des rechten Winkel die sogenannte Hypotenuse. Die verbleibenden zwei Seiten sind die Katheten. Die teilen sich noch einmal auf, so dass x bezogen auf den Winkel ? die Gegenkathete und die andere hier als Ankathete bezeichnet wird.
Gegenkathete
Sinus =
Hypotenuse
Das ist schon wieder so eine Gesetzmäßigkeit, auf die man sich in der Mathematik verlassen kann. Dieses Verhältnis aus Gegenkathete und Hypotenuse ist für einen bestimmten Winkel immer gleich, egal welche Ausmaße das rechtwinklige Dreieck annimmt.
Ankathete
Cosinus =
Hypotenuse
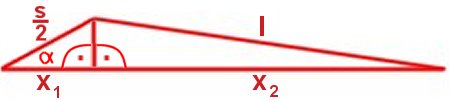
x1
cos ? =
s/2
x1 = s/2 · cos ?
Der Cosinus führt uns direkt zu der gesuchten Teilstrecke. Hier noch der Vollständigkeit halber die Formeln für Tangens und Cotangens:
Gegenkathete
tan ? =
Ankathete
Ankathete
cot ? =
Gegenkathete
Wenn wir jetzt einmal sehr grob abschätzend s/2 = 40 mm und für ? = 30° einsetzen, sollten knapp 35 mm für x1 herauskommen.

Den linken Teil haben wir jetzt. Allerdings ist für den rechten Teil doch jetzt x nötig:
x
cos ? =
s/2
x = s/2 · cos ?
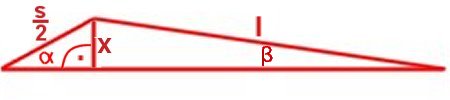
X
sin ? =
l
Den entsprechenden Term für x oben in diese Gleichung eingesetzt ergibt:
s/2 · cos ?
sin ? =
l
Mit einem Zahlenwert für sin(?) kann man so nichts anfangen. Man braucht den Winkel selbst. Und dazu gibt es die Umkehrfunktion mit der Vorsilbe 'arc'. Wenn Sie prüfen wollen, ob ein bestimmter Taschenrechner mit dieser Umkehrfunktion umgehen kann, sollten Sie auf den Tasten nicht nur nach 'arcsin' suchen, sondern auch nach 'asin' oder 'sin-1', Die letztgenannte Schreibweise ist nicht so günstig, weil man die auch als 1/sin missverstehen könnte.
Umkehrfunktion heißt aber, dass man nicht den Wert auf der x-Achse vorgibt und den entsprechenden auf der y-Achse sucht, sondern ausgehend von dem auf der y-Achse auf den x-Wert schließt. Unabhängig und abhängig Variable sind vertauscht.
Wenn wir jetzt, anknüpfend an das vorige Kapitel s/2 = 40 mm, für ? = 30° und l = 100 mm einsetzen, sollten etwa 20° für ? herauskommen. Funktioniert das nicht, dann liegt es vielleicht an der Einstellung des Taschenrechners. Der hat dann nicht den Winkel, sondern das zugehörige Bogenmaß (Radiant) ausgegeben. Hier die Umrechnung bezogen auf einen Kreis mit Radius 1 (Einheitskreis):
Bogenmaß = Winkel : 180° · ?
Winkel = Bogenmaß · 180° : ?
Hier wäre einmal wieder vorherige Abschätzung der Werte gefragt. Der Winkel ? muss deutlich kleiner als der Winkel ? sein, je größer ?, umso größer der Unterschied.
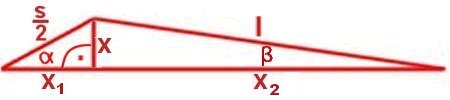
x2
cos ? =
l
x2 = l · cos ?
Jetzt ist einfach nur noch mit dem Cosinus 'x2' zu berechnen, was etwa 94 mm ergibt. Wenn man sich das Dreieck anschaut, wird klar, dass der Wert knapp unter dem für 'l' liegt. Der Kolben befindet sich 5 mm unterhalb von OT wegen der Schrägstellung der Kurbelwelle und 6 mm wegen der Schrägstellung der Pleuelstange, macht zusammen 11 mm.
Wichtig ist an diesen beiden Kapiteln, dass wir die Formel allgemein formulieren konnten. D.h. jemand, der eine solche Lösung für andere Kurbeltriebe bzw. Winkel braucht, muss nicht jedes Mal den ganzen beschriebenen Weg gehen. Er hat drei Formeln, setzt nach und nach seine Werte ein und erhält sein Ergebnis.
Die drei Formeln ließen sich auch jetzt schon zusammenfassen. Aber man will die Arcusfunktion zwischendrin vermeiden. Allerdings müssen Sie sich für die Berechnung komplett in einer Formel noch ein wenig gedulden.
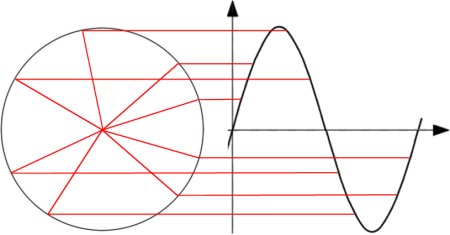
Links ist der Kreis mit dem Radius 1 dargestellt. Der Radius 1 hat den Vorteil, dass Sie nicht durch den Radius (die Hypotenuse) dividieren müssen. Unterschiedliche Radien sind zu sehen, der erste waagerecht nach rechts allerdings nicht. Von da aus wächst der Winkel ?. Wenn der Radius wieder rechts ankommt, hat der Winkel die 360° erreicht. Für jeden Winkel wurde die Höhe rechts im Diagramm abgetragen.
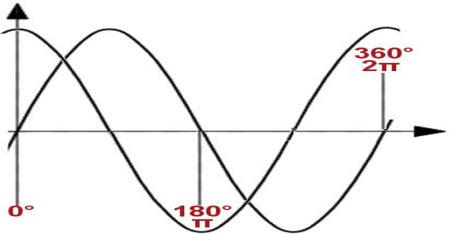
Hier noch einmal das Diagramm alleine. Es wird Sinusfunktion f(x) = sin ? genannt. Als Längen auf der x-Achse sind jetzt die jeweiligen Winkel bezeichnet. Zusätzlich finden Sie darunter die Umrechnungen in Längen vom Bogenmaß. Wichtig: die Funktion ist zu beiden Seiten endlos und sich alle 2 ? periodisch wiederholend.
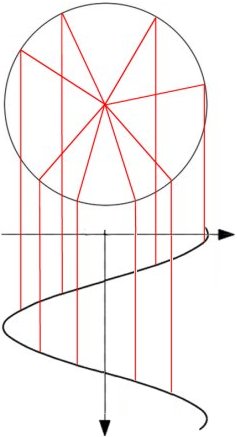
In diesem Bild wurde nicht wie oben beim Sinus die Gegenkathete, sondern wie beim Cosinus die Ankathete auf die Funktion f(x) = cos ? übertragen. Zusammenfassend: Aus den beiden Strecken, die durch einen Radius im Einheitskreis zur y- und zur x-Achse hin abgetragen werden, kann die Winkelfunktion definiert werden.

Hier sehen Sie die Graphen der Funktionen f(x) = sin(?) und f(x) = cos ? gemeinsam. Bei ?) = 0° ist der Sinus Null und der Cosinus 1, bei 180° der Sinus Null und der Cosinus -1 und bei 360° ist die Situation gleich der bei 0°. Der Sinus ist punktsymmetrisch zum Nullpunkt des Koordinatensystems. D.h. der positive Ast von f(x) = sin ? ergibt um dem Nullpunkt gedreht den negativen. Der Cosinus ist zur y-Achse klappsymmetrisch. Ihr positiver Teil über der y-Achse geklappt ergibt den negativen.
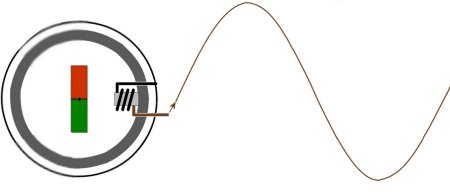
So das wäre jetzt eine Sinusfunktion in der Kfz-Praxis. Auch hier spielt der Kreis eine Rolle, denn der rotierende Stab-Dauermagnet nähert sich drehenderweise der auf der einen Seite mit Minus (Masse) verbundenen Wicklung einmal mit seinem Nordpol und dann wieder mit dem Südpol.
Im Moment ist keiner von beiden der Wicklung an nächsten, was beim Graphen der Sinusfunktion den Nulldurchgang bedeutet. Dreht er aber im Uhrzeigersinn weiter, dann strebt die Kurve dem Maximum zu.
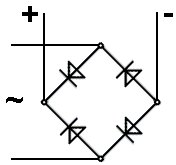
Erzeugt wird also immer Wechselspannung mit einer Sinusschwingung. Gespeichert werden kann aber nur Gleichspannung. Mit einer Diode würde der komplette negative Teil weggeschnitten. Um auch diesen noch nutzbar zu machen setzt man die obige Schaltung ein.
Jetzt ist der negative Teil der Sinuskurve nach oben geklappt. Aber Sie sehen, dass die erzielte Gleichspannung immer noch sehr unregelmäßig ist. Sollen als mittlere Spannung (gerade Linie) knapp 14 Volt garantiert sein, würden die Maxima vermutlich knapp über 20 Volt liegen. Als Ausweg gibt es die folgende Lösung:
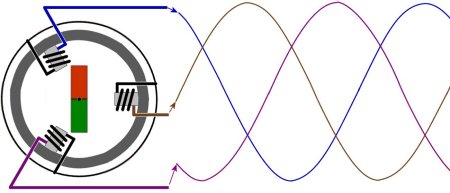
Hier erzeugen drei Spulen entsprechend viele Spannungen mit sinusförmigem Verlauf. Da sie exakt um 120° oder 2/3 ? gegeneinander versetzt sind, kann man durch eine Senkrechte zu jedem Zeitpunkt die Spannung verstimmen. Natürlich kann man die drei Drähte (Phasen) nur über je zwei Dioden an das Gleichstromnetz klemmen, weil sonst ein Kurzschluss entstünde.
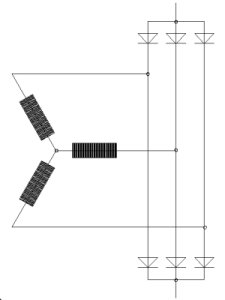
Aber man sieht doch deutlich die geringeren Abweichungen von einer optimal gleichmäßigen. Diese werden durch die Schaltung oben noch deutlich geringer, weil wieder die negativen Teile der Sinuskurven nach oben geklappt werden.

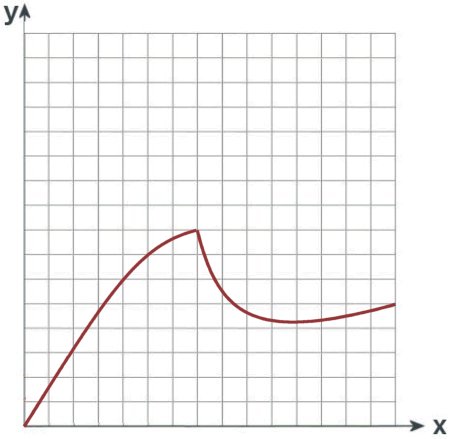
Bei Funktionen mit einem Knick, kann man natürlich im Knickpunkt keine eindeutige Tangente anlegen. Da die Ableitung einer Funktion wieder eine Funktion ist, die man z.B. zeichnerisch darstellen könnte, gibt es für die oben gezeichnete Funktion keine Ableitung. Gibt es eine, kann dann eine weitere Ableitung gebildet als f''(x) gebildet werden.
Zurück zu der Rechenregel bei einer Ableitung. Vielleicht ist es Ihnen auch schon aufgefallen. So entsteht aus
f(x) = x2
f'(x) = 2
Aus dem Exponenten wird der Multiplikator vor dem x und sie selbst um 1 verringert. Egal welche Konstante (also ohne x2 oder x) dahinter hängt, die verschwindet. Deshalb müsste dann aus
f(x) = x4
f'(x) = 4 x3
werden. Oder aus
f(x) = x5 + 13
f'(x) = 5 x4
Jetzt haben Sie als weitere Funktion schon den Sinus bzw. Cosinus kennengelernt. Wie ist denn dessen erste Ableitung? Wir verraten wir das Ergebnis vorher, nämlich
f(x) = sin x
f'(x) = cosin x
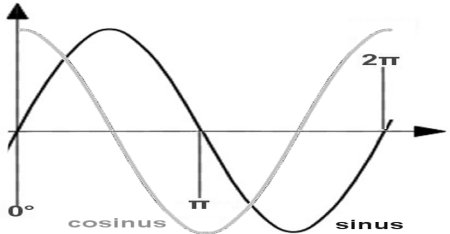
Die Sinuskurve beginnt bei f(x) = 0 die des Cosinus bei 1. Dann hat der Sinus im Nullpunkt die Steigung 1. Im obersten Punkt der Sinuskurve wird die Steigung dann Null, was der Cosinus ebenfalls exakt abbildet. Desgleichen im Punkt ? mit der Steigung -1.
Der Cosinus gibt also für jeden x-Wert exakt die Steigung der Sinuskurve wider. Jetzt bleibt nur noch die Frage nach der Ableitung für den Cosinus. Hier mal wieder diese und noch weitere Lösungen:
f(x) = cosin x
f'(x) = - sin x
f(x) = - sin x
f'(x) = - cosin x
f(x) = - cosin x
f'(x) = sin x
Oder hier noch verkürzt:
f(x) = sin x
f'(x) = cosin x
f''(x) = - sin x
f'''(x) = - cosin x
f(4)(x) = sin x
Und wieder zurück zu einem unserer Ursprungsbeispiele:
f(x) = x3
f'(x) = 3 x2
f''(x) = 3 · 2x
f'''(x) = 6
f(4)(x) = 0

Tank eines Mercedes Actros
Daimler lädt unabhängige Test-Journalisten zur frühjährlichen Fahrt die portugiesische Algarve entlang. Objekte sind ein Actros 1845 der 2. Generation und sein Vorgänger von 2015. Es soll eine Ersparnis von 6 Prozent nachgewiesen werden.
Anscheinend ohne irgendeine Möglichkeit der Manipulation spulten neben sonstigen Tests die jeweils aus zwei Fahrern bestehenden Teams die jeweils 100 km hin und zurück auf der Test-Autobahn A 22 zwischen Tavira und Lagos herunter. Sie wechselten sowohl sich ab wie die Auflieger und die Reihenfolge während der Fahrt.
Am Ende wurde der Tank ausgebaut und gewogen. Wer würde da noch skeptisch sein? Die Werte sind mit 132,7 kg zu 123,2 kg. Diese werden auf 30,5 und 28,8 Liter umgerechnet. Kann das sein? Aral gibt einen 'von den Motorherstellern eingeengten Dichtebereich von 820 bis 845 kg/m3' an.
Sie sehen, wir haben knapp den Mittelwert zwischen den beiden von Aral aufgezeigten Grenzen genommen und erhalten fast genau 160 Liter, was durch 400 km (2 Umläufe) geteilt 40 statt 30,5 Liter auf 100 km ergibt. Wie kann es sein, dass man sich bei einem solch umfangreichen Test so verrechnet?
Dabei bleibt die Ersparnis von ca. sechs Prozent doch erhalten, egal ob man in Kilogramm oder Liter und auch egal mit welcher Dichte man rechnet. Aber waren vielleicht die wahren Literzahlen mit z.B. 37 Liter/100km den Mercedes-Leuten unangenehm, oder war gar der ältere Actros verschlechtert worden, um den jüngeren in einem besseren Licht erscheinen zu lassen.

Das ist der Nissan Leaf, das meist verkaufte Elektroauto der Welt. Seine Daten interessieren uns jetzt nicht so sehr, sondern nur seine Batterie, 2017 auf 30 kWh gewachsen. Noch genauer gesagt interessiert uns die Batterie des Nissan Leaf, weil man sie zusammen mit dem Neufahrzeug sowohl mieten als auch kaufen kann.
Da stellt sich doch rein mathematisch sofort die Frage, was auf kürzere oder längere Sicht günstiger ist. Die Mietpreise sind sowohl jährlicher Fahrleistung als auch nach Laufzeit gestaffelt. Hier macht eigentlich nur die längst mögliche von 3 Jahren Sinn. Wir gehen bei einem Elektroauto von 15.000 Jahreskilometern aus.
Da die Preise für das Modell mit 30 kWh noch nicht feststehen, nehmen wir das mit 24 kWh. Das Verhältnis von Mieten zu Kaufen wird ähnlich sein. Beim Mieten wären monatlich 86 Euro zu entrichten. Auf Erfahrungswerten basiert die Schätzung des Kapazitätsverlusts von linear ca. 2 Prozent pro Jahr. Dann wären nach 10 Jahren nur noch 80 Prozent vorhanden, z.B. eine 30 kWh-Batterie auf 24 kWh gefallen.
Wir tauschen dann aus, obwohl wir natürlich weiter fahren könnten. Nissan ersetzt bei gemieteten Batterien erst bei 75 Prozent. Pro Jahr sind also 86 · 12 = 1.032 Euro fällig, in 10 Jahren 10.320 Euro. Neben den schon entrichteten 5.900 Euro beim Kauf wäre dann noch einmal die gleiche Summe fällig, macht zusammen 11.800 Euro. So gesehen ist Mieten günstiger. Geht man allerdings von Nissans 75 Prozent aus, steigt der Mietpreis auf 12.900 Euro und ist ungünstiger.
Eingezahlt Zinsverlust Eingezahlt Zinsverlust
1 1032 € 5.900 €
2 1032 € 20,64 € 118,00 €
3 1032 € 41,69 € 120,36 €
4 1032 € 62,75 € 122,77 €
5 1032 € 83,82 € 125,22 €
6 1032 € 104,88 € 127,73 €
7 1032 € 125,94 € 130,28 €
8 1032 € 147,00 € 132,89 €
9 1032 € 168,06 € 135,54 €
10 1032 € 189,12 € 5.900 € 138,26 €
10.320 € 943,90 € 11.800 € 1.151,05 €
Zugegeben, durch die Zinsrechnung wird es etwas komplizierter. Sicher scheint allerdings, dass es nicht während der nächsten 10 Jahre bei so niedrigen Zinsen bleiben wird. Wir haben oben kontinuierlich maßvolle 2 Prozent angenommen. Je höher, desto klarer schlägt das Pendel in Richtung Mieten aus, das auch schon bei null Zinsen ca. 1.500 € Unterschied ergibt.
Allerdings sind wir hier von einem Wechsel bei 80 Prozent verbliebener Kapazität ausgegangen. Bei 75 Prozent Restkapazität kehrt sich der Vorteil vollends in Richtung 'Kaufen', denn in der zweiten Spalte kommen theoretisch 2,5 mal 1032 € hinzu. Das ergibt in der zweiten Spalte 12.900 €, während in der vierten Spalte alles beim Alten bleibt.
Nimmt man die Zinsen hinzu, so zeigt schon die Tabelle oben, dass die Zinsen in der dritten Spalte über die in der fünften Spalte hinauswachsen. Wer hätte gedacht, dass der Zeitpunkt bzw. die Restkapazität beim Austausch eine solch wichtige Rolle spielt? Übrigens dürfte der Einfluss der Verbilligung von Batterien im Laufe der Zeit sich auf beide Rechnungen auswirken, denn immerhin hat der Hersteller alle drei Jahre ein Interesse an der Fortsetzung des Mietvertrages.
Kaum ein Hersteller, auch Nissan nicht, schreibt in sein Prospekt oder seine Preisliste, bei welcher Restkapazität er im Falle von Mieten austauscht und doch ist dieser Punkt von entscheidender Bedeutung. Hinzu kommen noch andere Vorteile des Kaufs der Batterie: Man muss keinen Vertrag beim Verkauf des Fahrzeugs übertragen, bzw. es werden keine schwierig zu berechnenden Ablösekosten fällig.
Abschied nehmen sollte man in beiden Fällen von der Möglichkeit, mit einer neuen Batterie mehr Kapazität zu erhalten, denn da hängt oft auch noch Hardware dran, die ebenfalls geändert werden müsste. Rein mathematisch müsste übrigens die Zinseszinsrechnung mindestens auch noch monatlich bezogen werden, was aber die Schlüsse daraus eher noch verstärkt hätte.
Allerdings darf man bei der Mathematik nicht die Kfz-Technik aus den Augen verlieren. Denn es ist doch sehr die Frage, ob bei einem 12,5 Jahre alten Elektroauto mit 187.500 km auf dem Buckel noch der Austausch einer teuren Batterie lohnt. Außerdem sind die Verträge über das Mieten von Batterien mit einer Reihe von Fußangeln gespickt. Wie immer lohnt sich genaues Durchlesen.

Das Bild oben ist Teil häufig vorkommender Arbeit für unsere Internetseiten. Es ist im (BMW-) Museum aufgenommen worden, gerade so, dass angesichts beschränkter Raumverhältnisse das Objekt der Begierde gerade noch vollständig eingefangen werden konnte. Schon bevor das Bild in diese Buchseite integriert werden konnte, musste es drastisch verkleinert werden, auch 'Skalierung' genannt.

Jetzt geht es darum, es für unsere Seiten zu präparieren. Im zweiten Bild sehen Sie schon einige erste Schritte der Bearbeitung, nämlich alles Überflüssige wegzuschneiden. Allerdings hat es immer noch diese durch die bewusste Schiefhaltung der Kamera bedingte Schräglage.
Eine Drehung um 20° bringt es in die richtige Position. Man bezeichnet den Vorgang auch als Rotation. Es an den Rändern zu beschneiden führt zum vorläufigen Endprodukt unten. Worum es aber in diesem Kapitel noch geht, ist das Nummernschild. Hier könnte man es möglicherweise belassen, aber bei einem willkürlich in der Öffentlichkeit aufgenommenen Fahrzeug geht das natürlich nicht.

Schauen Sie sich dieses verunglückte Nummernschild an. Es ist die originale Nummer getilgt und so ganz ohne konnte es nicht bleiben. Auch ist das Einsetzen des Baujahres bei diesem Oldtimer sicherlich eine gute Idee, aber allein nur Skalieren, Rotieren und Hinschieben (Translation) haben offensichtlich nicht gereicht.

Hier sehen Sie die Scherung als Lösung des Problems, ein Teil von Vielem, was ein gutes Grafikprogramm möglich macht. Doch wie löst es das Problem mit mathematischen Mitteln? Da ist zunächst einmal die Skalierung, die im Bild unten an zwei Rechtecken gezeigt wird. Zwischen beiden ist der Faktor 1/2 bzw. 2, je nachdem, ob man vom großen zum kleinen oder umgekehrt vorgeht.
Skalierung
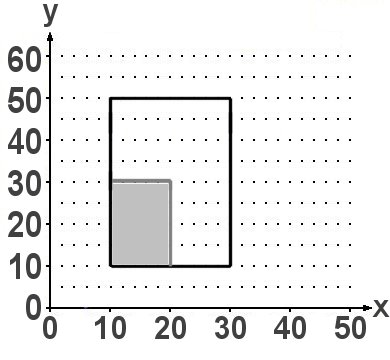
Obwohl wir das Bild des BMW-Oldtimers oben verkleinert haben, machen wir es hier der Einfachheit halber umgekehrt, wir vergrößern und nehmen dazu exemplarisch einen der drei Eckpunkte, die ihre Position verändern, oben links, oben rechts bzw. unten rechts. Der Punkt oben rechts hat die Koordinaten x=20 und y=30. Die schreiben wir platzsparender ein wenig anders:
Das 'r' mit dem Pfeil darüber ist ein sogenannter Ortsvektor. 'Vektoren' haben in der Mathematik zusätzlich zu einer bestimmten Größe auch nur eine Richtung, die es zu beachten gilt. Was nützt es, eine Kraft in N oder kN zu berechnen, wenn man ihre Wirkrichtung nicht kennt. Interessant wird es immer, wenn zwei möglicherweise auch unterschiedliche Kräfte in unterschiedliche Richtungen ziehen.
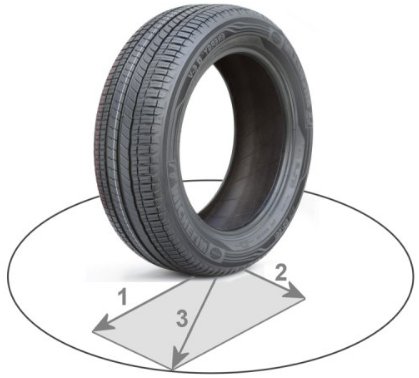
In der Kfz-Technik berühmt ist der Kamm'sche Kreis, wichtig für etwas extremere Kurvenfahrer/innen. '1' bezeichnet die Vortriebskraft, '2' die Seitenführungskraft am Rad. Beide sind noch weit von der durch den Kamm'schen Reibungskreis gezogenen Grenze entfernt. Entscheidend ist allerdings die Resultierende als Diagonale im Kräfteparallelogramm und die zeigt an, dass hier die Grenze der Übertragbarkeit erreicht ist. Bei der Skalierung muss die jeweilige x- und y-Komponente des Vektors mit dem Skalierungsfaktor multipliziert werden. Dabei lässt auch ein Grafikprogramm unterschiedliche Skalierungsfaktoren für x und y zu:
x' = x · dx
y' = y · dy
Translation
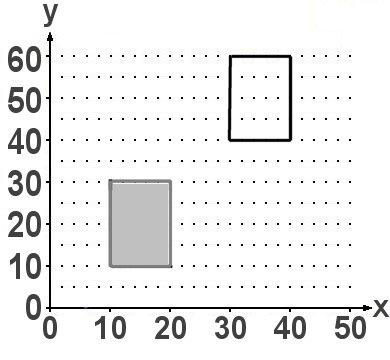
Bei der Translation (Verschiebung) unten kommt statt eines Skalierungsfaktors ein Verschiebevektor zum Einsatz. Hier wird deutlich, dass, wenn ein Vektor einmal nach Betrag und Richtung festgelegt ist, wann ihn auch verschieben kann, beim Kamm'schen Kreis z.B. 2 an das Ende von 1. Sie sehen, das Ergebnis ist das gleiche. Nehmen wir bei der Translation den Ortvektor nach x = 10, y = 10, dann kann man sich hier angreifend den Verschiebevektor nach x = 30, y = 40 vorstellen:
x' = x + dx
y' = y + dy
Rotation
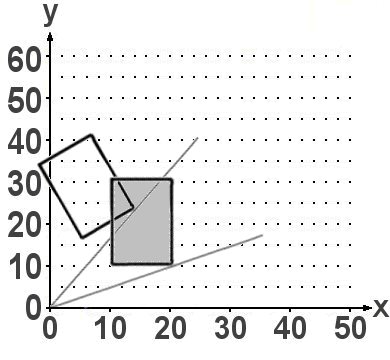
Rotiert (gedreht) wird hier um 30°. Wie der Kreisbogen zeigt, bleibt dabei die Länge x erhalten. Sie bildet im neu entstehenden Dreieck die Hypotenuse. So kann man jetzt den x-Anteil des neuen Punktes ausrechnen:
x' = x · cos ?
Wie Sie im Bild oben erkennen, ergibt die Berechnung des neuen x-Wertes ca. 35.
x' = (x · cos ?) - (y · sin ?)
y' = (y · sin ?) - (y · cos ?)
Scherung
Nun sind wir endlich bei der Scherung angelangt, dem eigentlichen Ausgangspunkt unserer Überlegungen. Das ? kennzeichnet das Maß der Verschiebung.
x' = x + (?x · y)
y' = y + (?y · x)
Das Ziel für dieses Kapitel ist relativ leicht zu beschreiben, der Weg etwas länger. Diesmal soll nicht nur die vom Kolben zurückgelegte Strecke in Abhängigkeit vom Kurbelwinkel ? in einer Formel berechenbar werden, sondern davon ausgehend auch noch je eine für die Kolbengeschwindigkeit und sogar die Beschleunigung erstellt werden. Also nicht die mittlere Kolbengeschwindigkeit ist gefragt, sondern die in jedem erdenklichen Punkt.
s = r·cos ? + l·cos ?
?s = r + l - r·cos ? - l·cos ?
Hier wird konsequent der Cosinus (Ankathete geteilt durch Hypotenuse) angewandt. Dabei ist s, wie oben in der Abbildung zu sehen, der momentane Abstand der Mitte des kleinen Pleuelauges von der Mitte der Hauptlager der Kurbelwelle. r + l kennzeichnet diesen Abstand, wenn der Kolben in OT steht- ?s ist demnach der Weg, den der Kolben (hier nach OT) noch zurückzulegen hat, also r + l - s.
r
? = -
l
sin ? = ? · sin ?
Man fasst r geteilt durch l als Pleuelverhältnis ? zusammen, kann also für die folgenden Überlegungen l vollständig ersetzen. Es kann die Werte 2 bis 3,5 erreichen, wobei die '2', also eine (zwischen den Pleuelaugen) nur doppelt so lange Pleuelstange schon sehr ehrgeizig wäre. Normale Gegengewichte wären dann wegen der Behinderung in UT schon nicht mehr möglich.
Dieses Bild stellt eine Verbindung zwischen dem unteren Dreieck über r und dem oberen über l her. Es veranschaulicht den berühmten Satz des Pythagoras, dass nämlich das Quadrat gebildet aus der Hypotenuse l (dunkelgrau) gleich der Summe der Quadrate ist, die aus den beiden Katheten gebildet werden (hellgrau).
l2 = r2 · sin2 ? + l2 · cos2 ?
l2 · cos2 ? = l2 - r2 · sin2 ?
r2 · sin2 ?
cos2 ? = 1 - -----
l2
Oben sehen Sie den Satz des Pythagoras ausgedrückt in den der Zeichnung entnommenen Termen. Im nächsten Schritt wurde auf beide Seiten erst r2 · sin2 ? subtrahiert und dann durch l2 geteilt. Jetzt kann man r2 geteilt durch l2 ersetzen und auf beiden Seiten die Wurzel ziehen. Heraus kommt:
?s = r + l - r·cos ? - l·cos ?
Das waren die vier Summanden, aus denen sich der zurückgelegte Weg des Kolbens ergab. r + l ist der Gesamtweg, von dem die beiden Katheten r·cos ? und l·cos ? (siehe Bild ganz oben) abgezogen werden müssen. Jetzt ersetzen wir cos ? und l durch r/?:
Halten Sie den Blick fest auf die vier Summanden gerichtet, dann sehen Sie, dass jeder von denen irgendwie mit r multipliziert ist. Man kann aus einer Summe solch einen Multiplikator herausholen. Das Verfahren nennt man Ausklammern. Das ergibt bei r nur eine 1, bei r/? jedes Mal 1/?, bei r·cos ? und bei nur noch cos ?. Danach werden die beiden Summanden 1/? und cos ? so vertauscht, dass sich 1/? im rechten Teil der Gleichung noch einmal ausklammern lässt.
Damit ist die Formel fertig, in die wir den Kurbelwinkel einsetzen können, um den bis dahin zurückgelegten Weg des Kolbens berechnen zu können. Nehmen Sie z.B. 40 mm für r, was dem halben Hub entspricht, und ? = 0,3, dann ergibt sich bei ? = 90° ein sin ? von 1 und ein cos ? von 0. Wenn Sie die Werte einsetzen, erhalten Sie für ?s exakt 40 mm, also genau die Mitte des Kolbenweges von 80 mm.
Jetzt gibt es aber ein Problem, nämlich mit der Wurzel. Wir müssen zur weiteren Berechnung der Kolbengeschwindigkeit und Kolbenbeschleunigung Ableitungen bilden, und das ist so nicht einfach möglich. Man kann in der Mathematik durchaus exakte Terme durch angenäherte ersetzen, muss allerdings den Fehler abschätzen. Und das machen wir hier mit einer 'Reihe'.
Der Sinn von 'Folgen' und 'Reihen' wird im Buch 'Mathematik' von Arens, Hettlich, Karpfinger, Lichtenegger und Stachel sehr schön beschrieben:
"Eine der wichtigsten Errungenschaften der Mathematik ist die konkrete Beschreibung vom Unendlichen. Dadurch wurde das Unendliche greifbar und mathematischen Aussagen zugänglich. Die Geschichte der Naturwissenschaften und Technik ist voll von Irrtümern, die man bei dem Versuch begann, Unendlichkeit zu fassen. Sie zeigen, wie komplex eigentlich unser heutiger Begriff des 'Grenzwerts' ist."
Wir benutzen jetzt eine Reihe von wesentlich einfacher formulierbaren Termen, um uns diesem Ausdruck zu nähern. Das Prinzip dieser Reihe soll an dem dritten, stark vereinfachten Term erläutert werden. Unten zeigen die beiden Formeln, auf welch einfache Form der Term gebracht werden kann.
Was haben Reihen und Folgen mit dem realen Leben zu tun. Sehr viel, wenn Sie z.B. manche Leute bei der Arbeit oder Freizeit betrachten. Auch man selbst macht sich bei etwas komplizierteren Tätigkeiten die beste Reihenfolge nicht klar, zumindest nicht vorher. Aber es gibt sie, die vernünftigste Vorgehensweise.
Unser ganzes Leben ist eine Abfolge von Tagen, Monaten und Jahren. Bisweilen denken wir sogar, die jetzige Situation schon einmal durchlaufen zu haben. Z.B. wenn wir uns einreden, etwas endgültig erledigt zu haben und es taucht als Problem doch wieder auf. In der Mathematik ist das alles aber viel profaner.
Da ist es einfach eine Folge von Objekten, die, anders als das menschliche Leben, auch unendlich sein kann. Das sind üblicherweise 'Abbilder' natürliche Zahlen, mit einem steigenden Index ausgestattet. In der Programmierung werden sie auch 'Arrays' genannt und recht oft der Reihe nach durchlaufen, beispielsweise um etwas zu suchen. Es wird Zeit, die Kurzschreibweise auszupacken:
Sie sehen, es muss nicht immer x als gesuchte Größe sein. Allerdings kommt 'n' als 'laufende' Größe wiederum oft vor. Dieser einfache Ausdruck erspart das Aufsummieren aller natürlichen Zahlen bis zur Größe 'n'. Statt des 'n' kann auch eine liegende '8' stehen, dann sind es alle Zahlen bis Unendlich.
Doch zurück zu unserer Wurzel aus 'x + 1'. Es geht darum, diesen Ausdruck daraufhin zu untersuchen, wie er sich verhält, wenn er durch eine Reihe ersetzt wird:
Da ? nur ?
1. Berechnen sie im Kopf 2,85 Prozent von 81,50 Euro! Dabei sollen Sie die Zahlen vorher sinnvoll runden, damit sie leichter zu rechnen sind.
Ergebnis: Euro.
2. Schätzen sie bitte ebenfalls ab, was der Grundwert bei einem Prozentwert von 21.500 Euro und 19 Prozent Mehrwertsteuer ist!
a) Etwas mehr als 19.000 Euro.
b) Etwas mehr als 18.000 Euro.
c) Etwas mehr als 17.000 Euro.
d) Etwas mehr als 16.000 Euro.
3. In welchem Bereich erwarten Sie das Drehmoment eines Motors, der bei 1500/min 500 kW leistet?
a) Bis 100 Nm.
b) 100 - 1000 Nm.
c) 1000 - 10.000 Nm.
d) Über 10.000 Nm.
4. Wo gehört das Komma hin?
Pi = 1.998 · 6.500 · 10,5 : 1.200.000 =
a) 1,1363625.
b) 11,363625.
c) 113,63625.
d) 1136,3625.
5. Mehrere richtige Antworten sind möglich!
b + c
a =
d
a) b = a · d + c
b) b = a · d - c
c) b = c · d + a
d) b = c · d - a
e) b = d · a + c
f) b = d · a - c
6. Die Kombination von Variablen, Zahlen und
Rechenzeichen ohne Gleichheitszeichen
nennt man (5 Buchstaben).
7. Das 'd' hinter dem senkrechten Strich ist in diesem Fall hier, . .
b · c
a = ? · d
d
a) auf beiden Seiten zu kürzen.
b) auf beiden Seiten zu multiplizieren.
c) auf der linken Seite zu multiplizieren, auf der rechten Seite zu kürzen.
d) auf der linken Seite zu kürzen, auf der rechten Seite zu multiplizieren.
a · d = b + c ? _ b
8. Die Variable b soll von der rechten auf die linke Seite gebracht werden.
Welches Rechenzeichen ist unmittelbar hinter dem senkrechten Strich anstelle des Unterstrichs einzusetzen?
a) Pluszeichen.
b) Minuszeichen.
c) Malzeichen.
d) Geteilt-Zeichen.
9. In welchen Fällen würde sich das Ergebnis des Terms ändern, wenn die Klammern weggelassen würden?
a) (a · b) = (c + d)
b) a · b = (c - d)
c) a · b = - (c + d)
d) a · b = - (c - d)
10. Nur eine Antwort ist richtig!
a · b + a · c = d ? - a · b
a) a · b = d + a · c
b) a · b = d - a · c
c) a · c = d + a · b
d) a · c = d - a · b
11. Mehrere richtige Antworten sind möglich!
Vh + Vc
? =
Vc
a) Vc (? + 1) = Vh
b) Vc (? - 1) = Vh
c) ? · Vc - Vc = Vh
d) ? · Vc + Vc = Vh
12. Mehrere richtige Antworten sind möglich!
ab
=
bd · bc
a) a
d · c
b) a
bd · c
c) a
d · bc
d) Der Term lässt sich nicht weiter zusammen-
fassen.
13. Nur eine Antwort ist richtig!
ab
=
bd - bc
a) a
d - c
b) a
d - c
c) a
bd - c
d) a
d - bc
e) Der Term lässt sich nicht weiter zusammenfassen.
14. Nur eine Antwort ist richtig!
a · b + b · c =
a) a (b + c)
b) b (a + c)
c) c (a + b)
d) Der Term lässt sich nicht weiter zusammenfassen.
15. Nur eine Antwort ist richtig!
b + c
a =
c
a) c (a + 1) = b
b) c (1 + a) = b
c) c (a - 1) = b
d) c (1 - a) = b
16. Mehrere richtige Antworten sind möglich!
1
a =
1 1
+
b c
a) a a
- = 1
b c
b) a a
+ = 1
b c
c) a a
+ = 1
c b
d) a a
- = 1
c b
17. Die Firma Mann + Hummel fertigt in einer Sekunde 16 Filter eines bestimmten Typs. Nehmen wir zwei Schichten, eine Fünf-Tage-Woche und Weiterfertigung während der Urlaubszeit an.
Wie viele Filter kommen so pro Jahr zusammen?
a) Ca. 240.000
b) Ca. 4 Mio.
c) Ca. 5,6 Mio.
d) Ca. 168 Mio.
e) Ca. 240 Mio.+
das Buch gefallen hat, wäre es nett, wenn Sie eine Kundenrezension schreiben würden.
Stichworte
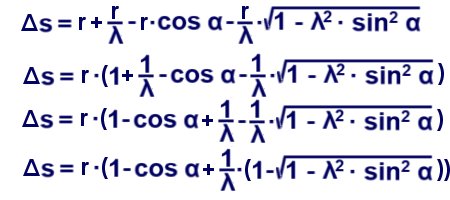
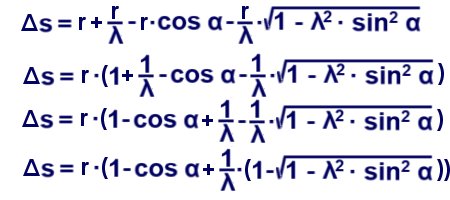





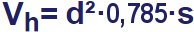

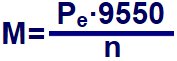




 | · d
| · d





 | · d
| · d